Perfect Lens Characteristics
Perfect Lens Characteristics - Java Tutorial
The simplest imaging element in an optical microscope is a perfect lens, which is an ideally corrected glass element that is free of aberration and focuses light onto a single point. This tutorial explores how light waves propagate through and are focused by a perfect lens.
The tutorial initializes with a parallel beam of light passing through the lens in coincidence with the optical axis and traveling from left to right. The Tilt Angle slider can be employed to tilt the axis of the light beam through ± 45 degrees, and the Focal Length slider adjusts the lens focal length values between 0.5 and 2.0 centimeters. A checkbox toggles simulations of plane and spherical wavefronts on and off, allowing the visitor to view how spherical waves are produced when a plane wavefront passes through the lens. The blue Reset button is utilized to re-initialize the tutorial.
Fundamental to the understanding of image formation in the microscope is the action of individual lens elements that comprise the components in the optical train. The simplest imaging element is a perfect lens (Figure 1), which is an ideally corrected glass element that is free of aberration and focuses light onto a single point. A parallel, paraxial beam of light passes through the converging lens and is focused, by refraction, into a point source located at the focal point of the lens (the point labeled Focus in Figure 1). Such lenses are often referred to as positive lenses because they induce a convergent light beam to converge more rapidly, or cause a divergent light beam to diverge less rapidly. A point source of light located at the lens focal point emerges as a paraxial, parallel beam of light as it leaves the lens, moving from right to left in Figure 1. The distance between the lens and the focal point is referred to as the focal length of the lens (denoted by the distance f in Figure 1).
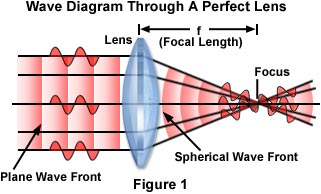
In a parallel beam of light, individual monochromatic light waves form a wavetrain having a combination of electric and magnetic vectors vibrating in phase to form a wavefront, which has a vibration orientation perpendicular to the direction of wave propagation. The plane wave is converted to a spherical wave as it passes through the perfect lens, with the front centered at the focal point (Focus) of the lens (Figure 1). Light waves arrive at the focal point in phase and interfere constructively with each other at this location. Alternatively, light comprising a spherical wavefront emanating from the focal point of a perfect lens is converted by the lens into a plane wave (proceeding from right to left in Figure 1). Each light ray in the plane wave undergoes a different change of direction upon encountering the lens because it arrives at the surface at a slightly different angle of incidence. Upon emerging from the lens, the direction of the light ray also changes. In real systems, the angle of refraction and focal point of a lens or group of lenses is dependent upon thickness, geometry, refractive index, and dispersion of each component in the system.
The general action of a perfect lens (or lens system) is to convert one spherical wave into another, with the geometrical properties of the lens determining the position of the focal point. As the distance of the light source from the lens is increased, the angle of diverging light rays entering the lens is decreased with a corresponding increase in the radius of the wavefront. If the radius of a spherical wave entering the lens is infinite, the radius of the spherical wave passing through the lens becomes equal to the focal length of the lens. A perfect lens has two focal points, and a plane wave passing through the lens is focused onto one of these points, depending upon whether the light rays enter from the left or right side of the lens.
In situations where the propagation direction of the plane wave does not coincide with the optical axis of the lens, the focal point of the spherical wave produced by the lens is also removed from the axis. When the Tilt Angle slider is activated, the tutorial illustrates the case of a plane wavefront encountering a perfect lens when tilted at an angle (α). The center of the resulting spherical wave is labeled S and lies at a distance δ from the axial focal point (labeled F in the tutorial), but within the same focal plane. The value of δ can be expressed as:
δ = f × sin(α)
where f is the focal length of the perfect lens. In terms of geometric optics, f is a value that refers to the radius of an arc centered on S and passing through the center of the lens as if it were a single refracting surface.
Sorry, this page is not
available in your country.



