Laser Energy Levels
Laser Energy Levels - Java Tutorial
A population inversion can be produced in a laser through two basic mechanisms, either by creating an excess of atoms or molecules in a higher energy state, or by reducing the population of a lower energy state. This tutorial explores metastable states for both three-level and four-level laser systems.
The tutorial initializes with two energy diagram windows representing a three-level (on the left) and a four-level laser (on the right). Positioned beneath the windows are a pair of blue Start buttons that can be used to initiate energy state transitions in each window separately or both windows together. A legend describing electron colors associated with energy states is positioned below the start buttons. To operate the tutorial, click on one of the start buttons and examine how electrons are promoted from the ground state to a highly excited state. After being excited, the electrons will migrate to a metastable state before proceeding through a laser transition back to the ground state (three-level laser) or to a lower laser energy level (four-level laser). The Applet Speed slider can be employed to adjust the tutorial execution sequence for a comfortable observation speed.
The most common approach for producing a population inversion in a laser medium is to add energy to the system in order to excite atoms or molecules into higher energy levels. Simply adding energy by thermally agitating the medium is not sufficient (under thermodynamic equilibrium) to produce a population inversion, because heat only increases the average energy of the population, but does not increase the number of species in the excited state relative to that in the lower state. The ratio of the number of atoms at two energy levels (1 and 2) under thermodynamic equilibrium is given by the following equation:
N2/N1 = exp [ - (E2 - E1) / kT]
where N(1) and N(2) are the number of atoms in level 1 and level 2, respectively, E(1) and E(2) are the energies of the two levels, k is the Boltzmann constant, and T is the temperature in kelvins. As demonstrated by the equation, at thermodynamic equilibrium, N(2) can be greater than N(1) only if the temperature is a negative number. Before the research describing maser and laser action was published, physicists referred to a population inversion as a negative temperature, which was symbolic of their view that any condition other than thermodynamic equilibrium was unlikely to be sustained.
To produce the required population inversion for laser activity, atoms or molecules must be selectively excited to specific energy levels. Light and electricity are the excitation mechanisms of choice for most lasers. Either light or electrons can provide the energy necessary to excite atoms or molecules to selected higher energy levels, and the transfer of energy is not required to directly promote electrons to a specific upper level of the laser transition. Some approaches can be rather complex, but these often produce better-performing lasers. One frequently utilized approach excites an atom or molecule to a higher energy level than required, after which it drops to the upper laser level. Indirect excitation can be employed to excite atoms in a surrounding gas mixture, which then transfer their energy to the atoms or molecules responsible for producing the laser action.
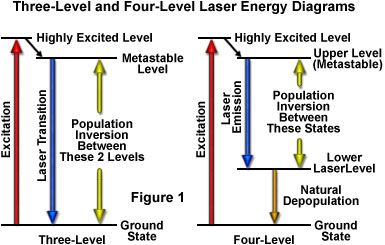
As previously discussed, the amount of time spent by an atom or molecule in an excited state is critical in determining whether it will be stimulated to emission and participate in a cascade of photons, or lose its energy through spontaneous emission. Excited states commonly have lifetimes of only nanoseconds before they release their energy by spontaneous emission, a period that is not lengthy enough to likely undergo stimulation by another photon. A critical requirement for laser action, therefore, is a longer-lived state that is suitable for the upper energy level. Such states do exist for certain materials, and are referred to as metastable states (see Figure 1). The average lifetime before spontaneous emission occurs for a metastable state is on the order of a microsecond to a millisecond, quite a lengthy period of time on the atomic timescale. With lifetimes this long, excited atoms and molecules can produce significant amounts of stimulated emission. Laser action is only possible if the population builds up faster than it decays in the upper energy level, maintaining a population larger than that of the lower level. The longer the spontaneous emission lifetime, the more suitable a molecule or atom is for laser applications.
The simplest functional energy-level structure for laser operation is a three-level system, which is illustrated in Figure 1(a). In this system, the ground state is the lower laser level, and a population inversion is created between this level and a higher-energy metastable state. Most of the atoms or molecules are initially excited to a short-lived high-energy state that is higher than the metastable level. From this state they quickly decay to the intermediate metastable level, which has a much longer lifetime than the higher energy state (often on the order of 1000 times longer). Because each atom's residence time in the metastable state is relatively long, the population tends to increase and leads to a population inversion between the metastable state and the lower ground state (which is continuously being depopulated to the highest level). Stimulated emission results from the fact that more atoms are available in the upper excited (metastable) state than in the lower state where absorption of light would most likely occur.
Although the three-level laser system works for all practical purposes, as exemplified by the first laser, a number of problems limit the effectiveness of this approach. The central problem occurs because the lower laser level is the ground level, which is the normal state for most atoms or molecules. In order to produce the population inversion, a majority of ground state electrons must be promoted to the highly excited energy level, requiring a significant input of external energy. In addition, the population inversion is difficult to sustain for an appreciable time, and therefore, three-level lasers must be operated in pulsed mode rather than continuously.
Lasers utilizing four or more energy levels avoid some of the problems mentioned above, and therefore are more commonly utilized. Figure 1(b) illustrates a four-level scenario. The energy level structure is similar to that in the three-level system, except that after the atoms drop from the highest level to the metastable upper state, they do not drop all the way to the ground state in a single step. Because the population inversion is not created between the ground state and the upper level, the number of atoms or molecules that must be elevated is dramatically reduced in this model. In a typical four-level laser system, if only one or two percent of the atoms or molecules reside in the lower laser level (which is above the ground state), then exciting only two to four percent of the total to the higher level will achieve the required population inversion. Another advantage of separating the lower laser level from the ground level is that the lower level atoms will naturally fall to the ground state. If the lower laser level has a lifetime that is much shorter than the upper level, atoms will decay to the ground level at a rate sufficient to avoid accumulation in the lower laser level. Many of the lasers designed under these constraints can be operated in a continuous mode to produce an uninterrupted beam.
Sorry, this page is not
available in your country.



