Refraction by an Equilateral Prism
Refraction by an Equilateral Prism - Java Tutorial
Visible white light passing through an equilateral prism undergoes a phenomenon known as dispersion, which is manifested by wavelength-dependent refraction of the light waves. This interactive tutorial explores how the incident angle of white light entering the prism affects the degree of dispersion and the angles of light exiting the prism.
The tutorial initializes having white light incident on a single face of an equilateral prism at a 40-degree angle with respect to a perpendicular line drawn from the prism face. In order to vary the incident angle, use the mouse cursor to translate the Incident Angle slider, which will also produce a corresponding change in the exit angles (θ(d)) of the light rays dispersed by the prism. The Refractive Index slider can be utilized to vary the prism refractive index between a value of 1.40 and 2.00, increasing the exit angles of light rays refracted by the prism.
The first demonstration of refraction and dispersion in a triangular prism was performed by British physicist Sir Isaac Newton in the late 1600s. Newton showed that white light could be dissected into its component colors by an isosceles prism having equal sides and angles. In general, a refracting or dispersing prism has two or more plane surfaces that are oriented in a manner favorable to refraction rather than reflection of incident light beams. When a light ray strikes the surface of a dispersing prism, it is refracted upon entering according to Snell's law and then passes through the glass until the second interface is reached. Once again, the light ray is refracted and emerges from the prism along a new path (see Figure 1). Because the prism alters the propagation direction of light, waves passing through a prism are said to be deviated by a specific angle, which can be very precisely determined by applying Snell's law to the geometry of the prism. The deviation angle is minimized when the light wave enters the prism with an angle that allows the beam to traverse through the glass in a direction parallel to the base.
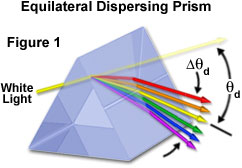
The amount of light deviation by a prism is a function of the incident angle, the prism apex (top) angle, and the refractive index of the material from which the prism is constructed. As prism refractive index values are increased, so is the deviation angle of light passing through the prism. Refractive index is often dependent upon the wavelength of light, with shorter wavelengths (blue light) being refracted at greater angles than longer wavelengths (red light). This variation of the deviation angle with wavelength is referred to as dispersion, and is responsible for the phenomenon that Newton observed over 300 years ago. Dispersion can be fine-tuned by selecting glasses with the appropriate refractive index characteristics for a particular application. In general, the dispersion properties of various glass formulations are compared through Abbe numbers, which are determined by measuring the refractive indices of specific reference wavelengths passed through the glass.
Sorry, this page is not
available in your country.



