Interférence

L’interférence de la lumière désigne le phénomène dans lequel plusieurs ondes lumineuses interagissent les unes avec les autres dans certaines circonstances, ce qui entraîne l’augmentation ou la diminution de leur amplitude combinée. Dans cet article, nous discutons à la fois de l’interférence constructive et de l’interférence destructive des ondes lumineuses, évoquons ce qui provoque les interférences et faisons part de quelques expériences et exemples concrets qui démontrent ce phénomène.

Qu’est-ce que l’interférence des ondes lumineuses ?

Une caractéristique importante des ondes lumineuses est leur capacité, dans certaines circonstances, à interférer entre elles. Selon leur définition en physique, les interférences sont la superposition des ondes, qui entraîne une augmentation ou une diminution de l’amplitude de l’onde résultante. Dans notre vie de tous les jours, nous observons presque tous différents types d’interférence optique, sans avoir conscience cependant de ce qui produit ce phénomène. L’un des meilleurs exemples de l’interférence de la lumière est illustré par la lumière réfléchie par une couche d’huile flottant à la surface de l’eau. Autre exemple : la bulle de savon illustrée à la figure 1, qui reflète tout un éventail de belles couleurs lorsqu’elle est éclairée par une source de lumière naturelle ou artificielle.

Quelle est la différence entre les interférences constructives et les interférences destructives ?

Cette interaction dynamique des couleurs découle de la réflexion simultanée de la lumière sur les surfaces intérieure et extérieure de la bulle (figure 1). Les deux surfaces sont très proches l’une de l’autre (la bulle ne fait que quelques microns d’épaisseur), et la lumière réfléchie par la surface intérieure interfère de manière constructive et destructive avec la lumière réfléchie par la surface extérieure. Cela s’explique par le fait que la lumière réfléchie par la surface intérieure de la bulle doit aller plus loin que la lumière réfléchie par la surface extérieure. Lorsque les ondes lumineuses réfléchies par les surfaces intérieure et extérieure se combinent, elles interfèrent les unes avec les autres, ce qui a pour effet de supprimer ou de renforcer certaines parties de la lumière blanche selon que l’interférence est destructive ou constructive. Cela entraîne les variations de couleurs reflétées par la bulle. Lorsque la distance supplémentaire parcourue par les ondes lumineuses internes est exactement égale à la longueur d’onde des ondes lumineuses externes, elles se recombinent de manière constructive et les couleurs vives de ces longueurs d’onde deviennent visibles. Dans les endroits où les ondes sont décalées, des interférences destructives se produisent, ce qui annule la lumière réfléchie (et la couleur).

Comment se produit l’interférence de la lumière ?

Voici une explication de la façon dont les ondes lumineuses interfèrent les unes avec les autres. Considérons une paire d’ondes lumineuses provenant de la même source qui se déplacent, par exemple, dans la direction D. Il s’agit de la direction de propagation (comme représenté à la figure 2), et si les vibrations (qui sont perpendiculaires à la direction de propagation et sont représentées par C à la figure 2) sont parallèles entre elles et sont également parallèles par rapport à la direction de la vibration, les ondes lumineuses peuvent alors interférer les unes avec les autres. Si les vibrations ne sont pas dans le même plan et vibrent à 90° l’une par rapport à l’autre, elles ne peuvent pas interférer l’une avec l’autre.

Interférence constructive

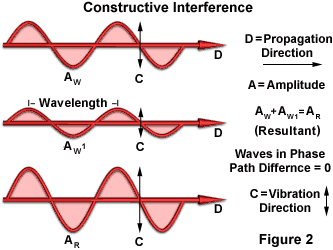
En supposant que tous les critères indiqués ci-dessus soient satisfaits, les ondes peuvent interférer soit de manière constructive, soit de manière destructive. Si les pics de l’une des ondes coïncident avec les pics de l’autre, les amplitudes s’ajoutent. Si les amplitudes des deux ondes sont égales, l’amplitude résultante sera le double de l’amplitude de chacune des ondes. N’oubliez pas que l’intensité lumineuse varie directement en fonction du carré de l’amplitude. Donc si l’amplitude est doublée, l’intensité est quadruplée. Cette interférence additive est appelée interférence constructive (illustrée à la figure 2).

Interférence destructive

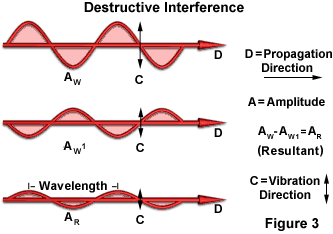
Si les pics d’une onde coïncident avec les creux de l’autre onde, l’amplitude obtenue diminue, voire est complètement annulée, comme illustré à la figure 3. On parle dans ce cas d’interférence destructive. Cela résulte en une baisse de l’intensité, ou dans le cas d’une annulation totale, en l’absence de lumière (noir).

Découvrez comment deux ondes lumineuses peuvent se combiner pour produire des interférences entre elles.

Démarrer le tutoriel

Exemples d’interférences

Thomas Young, un physicien du début du XIX^e siècle, a mis en évidence l’interférence en montrant que la lumière est un phénomène ondulatoire, et il a également postulé que les différentes couleurs de la lumière provenaient d’ondes de longueurs différentes. Cela était contraire à l’opinion communément admise à l’époque, largement orientée en faveur de la théorie selon laquelle la lumière est un flux de particules. En 1801, Young a réalisé une expérience apportant des preuves importantes que la lumière visible a des propriétés ondulatoires. Cette expérience classique, souvent appelée « l’expérience de la double fente », utilisait à l’origine comme source de lumière la lumière du soleil diffractée dans un premier temps par un passage dans une première fente. Mais nous décrirons l’expérience en utilisant une lumière laser rouge cohérente.

L’expérience de la double fente

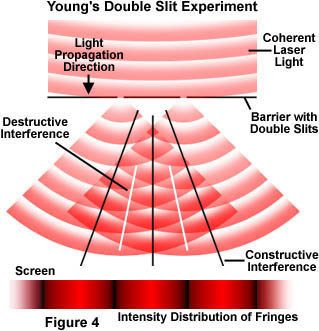
Le dispositif de base de l’expérience de la double fente est représenté à la figure 4. Une lumière laser cohérente vient éclairer une barrière contenant deux ouvertures en forme de trou d’épingle qui ne laissent passer qu’une partie de la lumière. Un écran est placé dans la zone située derrière les fentes et une figure d’interférence alternant des franges rouge vif et des franges noires devient visible sur l’écran. La clé de cette expérience tient dans la cohérence mutuelle entre la lumière diffractée par les deux fentes de la barrière. 

Découvrez comment les figures d’interférence changent en fonction de la longueur d’onde et de la distance entre les fentes.

Démarrer le tutoriel

Que sont les franges d’interférence ?

Lorsque la lumière laser est diffractée à travers les deux fentes de la barrière, chaque onde diffractée rencontre l’autre en une série d’étapes, comme illustré à la figure 4 (et graphiquement dans le tutoriel interactif décrit ci-dessus). Les ondes se rencontrent parfois en phase (il y a interférence constructive), parfois décalées ou déphasées (il y a interférence destructive), et parfois partiellement en phase. Lorsque les ondes se rencontrent en phase, elles s’additionnent du fait des interférences constructives, et une zone lumineuse apparaît sur l’écran. Dans les zones où les ondes se rencontrent en décalage total, elles se soustraient les unes des autres du fait des interférences destructives, et une zone sombre apparaît dans cette partie de l’écran. Les figures résultantes sur l’écran, qui sont le produit de l’interférence entre les deux faisceaux diffractés de la lumière laser, sont souvent appelées franges d’interférence.

D’autres types d’expériences ont été conçus pour démontrer la nature ondulatoire de la lumière et les effets de l’interférence. Les plus notables sont l’expérience à un miroir de Humphrey Lloyd et les expériences à deux miroirs et à biprisme conçues par Augustin Fresnel. Ces expériences sont décrites en détail dans de nombreux ouvrages de physique indiqués dans notre bibliographie.

L’expérience des anneaux de Newton

Sir Isaac Newton, le célèbre mathématicien et physicien du XVII^e siècle, fut l’un des premiers scientifiques à étudier les phénomènes d’interférence. Dans sa célèbre expérience des anneaux, Newton a placé une lentille convexe de grand rayon de courbure sur une plaque de verre plate et a appliqué une pression pour maintenir la lentille et la plaque de verre ensemble. Lorsqu’il a observé les plaques à travers la lumière du soleil réfléchie, il a observé une série de bandes concentriques très colorées lumineuses et foncées semblables à celles illustrées à la figure 5. Newton a compris que les anneaux indiquaient la présence d’un certain degré de périodicité et a utilisé cette observation pour suggérer une théorie ondulatoire de la lumière. Newton considérait néanmoins que la lumière était un flux de particules.

Les anneaux se forment en raison de la fine couche d’air qui existe entre les surfaces courbes convexes de la lentille et les surfaces plates de la plaque de verre. La lumière réfléchie par les surfaces supérieure et inférieure du verre se superpose (se combine) et produit des figures d’interférence sous la forme d’anneaux colorés. Ce principe est souvent utilisé par les fabricants de lentilles pour tester l’uniformité de grandes surfaces polies.

Distribution des franges et de l’intensité des interférences

Les franges d’interférence à distribution d’intensité (comme celles observées dans l’expérience de la double fente de Young) varient en intensité lorsqu’elles sont présentées sur un fond uniforme. La visibilité (V) de l’intensité a été définie par Albert Michelson, physicien du début du XX^e siècle, comme la différence entre l’intensité maximale et l’intensité minimale d’une frange divisée par leur somme :

V = I(max) - I(min)/I(max) + I(min)

Où I(max) est l’intensité maximale et I(min) l’intensité minimale. À partir de l’équation, l’intensité de la frange idéalisée se situe toujours entre zéro et un, mais dans la pratique, la visibilité de la frange dépend de la géométrique du dispositif expérimental et de la plage spectrale utilisée. Celles-ci sont responsables de la myriade de figures d’interférence observées dans les événements naturels.

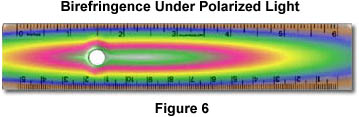
Les couleurs d’interférence provenant des zones sous contraintes dans les matériaux peuvent être facilement observées en lumière polarisée. La règle illustrée dans la figure 6 est une règle en plastique observée à travers des polariseurs croisés. Sous une lumière normale, la règle est translucide et ses graduations sont clairement visibles. Cependant, lorsqu’elle est observée en lumière polarisée, la règle présente des figures de contrainte qui apparaissent plus profondes dans les zones plus fortement déformées. Ceci est dû à un degré élevé d’alignement des molécules des polymères à longue chaîne dont la règle est composée. Notez que le plus grand degré de biréfringence se trouve près du trou sur le côté gauche de la règle.

Utilisations concrètes de l’interférence de la lumière

Parmi les autres utilisations de l’interférence de la lumière, on peut citer les mesures effectuées sur de longues distances avec des lasers. Dans ce cas, les lasers peuvent être utilisés pour mesurer de très petites distances sur une plage de plusieurs kilomètres. Pour ce faire, il suffit de diviser le faisceau laser et de le faire se réfléchir sur différentes surfaces. L’analyse des franges d’interférence résultantes (lors de la recombinaison des faisceaux laser divisés) permet d’obtenir un calcul remarquablement précis de la distance entre les deux objets.

Les hologrammes dépendent également de l’interférence de la lumière pour produire leurs images tridimensionnelles. Dans les hologrammes à réflexion, un faisceau de référence et un faisceau éclairant un objet sont tous deux réfléchis sur un film épais par deux côtés opposés. Ces faisceaux interfèrent pour produire des zones claires et sombres qui correspondent à une image qui apparaît en trois dimensions. Les hologrammes à transmission utilisent à la fois le faisceau de référence et le faisceau éclairant l’objet du même côté du film pour produire un type d’effet similaire.

L’interférence se produit également avec des ondes sonores ou encore les vagues créées dans un bassin d’eau stagnante. Une expérience d’interférence très concise et simple peut être réalisée à la maison au moyen d’un évier plein d’eau et de deux billes. Tout d’abord, attendez que l’eau soit parfaitement immobile, puis lâchez simultanément les billes dans l’eau (séparées d’environ 25-35 cm) d’une hauteur d’environ 30 cm. Tout comme pour les ondes de lumière, les deux billes induiront une série de vagues dans l’eau se propageant dans toutes les directions. Les vagues qui se forment dans la zone située entre les points où les billes sont entrées dans l’eau finiront par entrer en collision. Lorsqu’elles se rencontrent sans décalage, elles s’additionnent de manière constructive pour faire une vague plus importante, et lorsqu’elles se rencontrent en décalage, elles s’annulent mutuellement de manière destructive. Faites l’expérience !