Introduction to Lasers
In popular science fiction movies during the 1950s, monsters were often portrayed that could emit lethal rays of light from their eyes (Figure 1), but until the invention of the laser, such concentrated and powerful energy beams were only fantasy. Now it is possible to modify, probe, or destroy matter using the highly focused radiation from energy sources known as lasers. Nearly all light that we see in our daily lives, ranging from the sun, stars, incandescent and fluorescent lamps, to even our television sets, occurs spontaneously when atoms and molecules rid themselves of excess energy.

Ordinary natural and artificial light is released by energy changes on the atomic and molecular level that occur without any outside intervention. A second type of light exists, however, and occurs when an atom or molecule retains its excess energy until stimulated to emit the energy in the form of light. Lasers are designed to produce and amplify this stimulated form of light into intense and focused beams. The word laser was coined as an acronym for Light Amplification by the Stimulated Emission of Radiation. The special nature of laser light has made laser technology a vital tool in nearly every aspect of everyday life including communications, entertainment, manufacturing, and medicine.
Albert Einstein may inadvertently have taken the initial step in laser development by realizing that two types of emission are possible. In an article published in 1917, he was the first to suggest the existence of stimulated emission. For many years physicists thought that the spontaneous emission of light was the most likely and dominant form, and that any stimulated emission would always be much weaker. It was not until after World War II that the search began for conditions that were necessary for stimulated emission to dominate, and to make one atom or molecule stimulate many others to produce the effect of amplifying emitted light.
A scientist at Columbia University, Charles H. Townes, was the first to succeed in amplification of stimulated radiation in the early 1950s, but his work centered around microwaves (with a much longer wavelength than visible light), and he termed his device a maser. Other scientists followed in building successful masers, and a significant amount of effort was concentrated into attempts to produce stimulated emission at shorter wavelengths. Many of the primary concepts for producing a laser were developed at about the same time, later in the 1950s, by Townes and Arthur Schawlow (of Bell Laboratories), and by Gordon Gould at Columbia University. Gould filed a patent application rather than publish his ideas, and although he was given credit for coining the word "laser" in his notebooks, almost 30 years passed before he was awarded several patents. There is still disagreement over who deserves credit for the concept of the laser. Two Soviets, Nikolai Basov and Aleksander Prokhorov, shared the 1964 Nobel Prize in physics with Townes for their pioneering work on the principles underlying masers and lasers. Schawlow was awarded a share of the 1981 Nobel Prize in physics for his laser research.
Publication of Townes' and Schawlow's work stimulated a huge effort to build a working laser system. In May of 1960, Theodore Maiman, working at Hughes Research Laboratories, built a device using a synthetic ruby rod that has been credited as being the first laser. Maiman's ruby laser emitted intense pulses of coherent red light at 694 nanometers in a tightly concentrated narrow beam, quite typical of the characteristics displayed by many current lasers. The first laser employed a small ruby rod having the ends silvered to reflect light, surrounded by a helical flash lamp, and was small enough to be held in the hand. Interestingly, the photographer commissioned by Hughes to publicize the discovery thought that the actual laser was too small and had Maiman pose with a larger laser that was not operational until later. Photographs showing Maiman with the "more impressive" laser are still circulated and used in many publications.
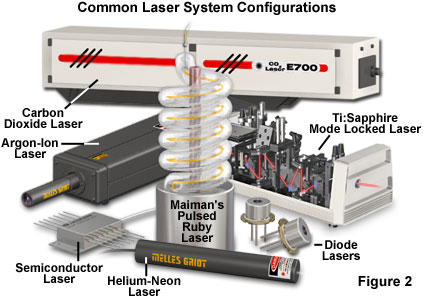
Although lasers emitting visible light are the most common, the basic principles are applicable through much of the electromagnetic spectrum. The first stimulated emission was achieved in the microwave region of the spectrum, but now lasers are available that emit ultraviolet and infrared light, and progress is being made toward producing lasers for the x-ray spectral region. Actual lasers in use today range in power output from less than a milliwatt to many kilowatts of continuous output, and some produce trillions of watts in extremely short pulses. Figure 2 presents some examples of representative lasers, which vary widely in size and application. Military and other research laboratories have built lasers that occupy entire buildings, while the most common lasers use a semiconductor device about the size of a sand grain.
An understanding of certain fundamental principles is essential in any explanation of how stimulated emission is produced and amplified. The first of these principles is necessary because the laser is inherently a quantum mechanical device and the quantum nature of energy must be invoked in order to explain the laser's operation. Classical physics assumes that energy can vary continuously and smoothly and that atoms and molecules can have any amount of energy. Einstein's work, which became key to the development of quantum mechanics, holds that energy exists in discrete units or quanta and that atoms and molecules (and therefore everything else) are restricted to having only certain discrete amounts of energy.
Several additional concepts, which originate at the photon and atomic level and are derived from the principle of quantization, are necessary in understanding laser operation:
- Quantization of energy in the atom results in discrete energy levels associated with the atom.
- Transitions from one energy level to another must be possible in order for light emission to occur.
- Several types of transition occur and affect the amount of energy involved in a transition.
- Spontaneous and stimulated emission is possible from energy transitions.
- Population inversions among energy levels must be achieved to amplify the stimulated emission of energy.
If an atom or molecule lies in an energy state that is higher than the lowest, or ground level state, it can spontaneously drop to a lower level without any outside stimulation. One possible result of dropping to a reduced energy state is the release of the excess energy (equaling the difference in the two energy levels) as a photon of light. Excited atoms or molecules have a characteristic spontaneous emission time, which is the average time that they remain in the excited higher energy state before they drop to a lower energy level and emit a photon. The emission time is an important factor in producing stimulated emission, the second type proposed by Einstein.
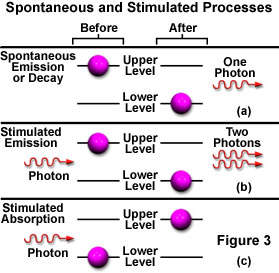
While in the excited state, if the atom is illuminated with an incoming photon having exactly the same energy as the transition that would spontaneously occur, the atom may be stimulated by the incoming photon to return to the lower state and simultaneously emit a photon at that same transition energy. A single photon interacting with an excited atom can therefore result in two photons being emitted. If the emitted photons are viewed as a wave, the stimulated emission will oscillate at the incoming light's frequency and be in phase (coherent), resulting in amplification of the original light wave's intensity. Figure 3 illustrates spontaneous (a) and stimulated (b) emission with the two coherent waves that result from the latter case.
The primary problem in achieving stimulated laser emission is that, under normal conditions of thermodynamic equilibrium, the population, or number of atoms or molecules at each energy level, is not favorable to stimulated emission. Because of the tendency of atoms and molecules to spontaneously drop to lower energy levels, the number at each energy level decreases as the energy increases. In fact, under normal conditions, for a transition energy corresponding to a typical optical wavelength (on the order of 1 electron-volt), the ratio of the number of atoms or molecules in the higher energy state to the number in the lower ground state is perhaps 10 E+17. In other words, virtually all of the atoms or molecules are in the ground state for a visible-wavelength energy transition.
The reason that stimulated emission is difficult to achieve becomes apparent when considering the likely events surrounding the decay of an electron from an exited state with the subsequent and spontaneous emission of light. The emitted light could easily stimulate emission from another exited atom, but so few are available that the emission more likely will first encounter an atom in the ground state, and will be absorbed instead (Figure 3(c)). Because the number of atoms in an exited state is so miniscule in relation to the number in the ground state, the emitted photon has a much greater probability of being absorbed, rendering stimulated emission insignificant when compared to spontaneous emission (at thermodynamic equilibrium).
The mechanism by which stimulated emission can be made to dominate is to have more atoms in the excited state than in the lower energy state, so that emitted photons are more likely to stimulate emission than to be absorbed. Because this condition is the inverse of the normal equilibrium situation, it is termed a population inversion. As long as there are more atoms in the upper energy level than in the lower, stimulated emission can dominate, and a cascade of photons results. The first emitted photon will stimulate the emission of more photons, these subsequently stimulate the emission of still more, and so on. The resulting cascade of photons grows, resulting in the amplification of emitted light. If the population inversion terminates (the ground state population becomes dominant), spontaneous emission will again become the favored process.
At the time of Einstein's proposal, most physicists believed that any condition other than thermodynamic equilibrium was unstable and could not be sustained. It was not until after World War II that serious consideration was given to methods of producing the population inversions necessary to sustain stimulated emission. Atoms and molecules can occupy many energy levels, and although some transitions are more likely than others (due to rules of quantum mechanics and for other reasons), a transition can occur between any two levels. The minimum requirement for stimulated emission and amplification, or laser action, is that at least one higher energy level must have a greater population than a lower level.
A population inversion can be produced through two basic mechanisms, either by creating an excess of atoms or molecules in a higher energy state, or by reducing the population of a lower energy state. A system can also be chosen that is unstable in the lower level, but for continuous laser operation, attention must usually be paid to both populating the higher level and depopulating the lower level. If too many atoms or molecules accumulate in the lower energy level, the population inversion will be lost and laser action will stop.
The most common approach for producing a population inversion in a laser medium is to add energy to the system in order to excite atoms or molecules into higher energy levels. Simply adding energy by thermally agitating the medium is not sufficient (under thermodynamic equilibrium) to produce a population inversion, because heat only increases the average energy of the population, but does not increase the number of species in the excited state relative to that in the lower state. The ratio of the number of atoms at two energy levels (1 and 2) under thermodynamic equilibrium is given by the following equation:
N2/N1 = exp[- (E2 - E1) / kT]
where N(1) and N(2) are the number of atoms in level 1 and level 2, respectively, E(1) and E(2) are the energies of the two levels, k is the Boltzmann constant, and T is the temperature in kelvins. As demonstrated by the equation, at thermodynamic equilibrium, N(2) can be greater than N(1) only if the temperature is a negative number. Before the research describing maser and laser action was published, physicists referred to a population inversion as a negative temperature, which was symbolic of their view that any condition other than thermodynamic equilibrium was unlikely to be sustained.
To produce the required population inversion for laser activity, atoms or molecules must be selectively excited to specific energy levels. Light and electricity are the excitation mechanisms of choice for most lasers. Either light or electrons can provide the energy necessary to excite atoms or molecules to selected higher energy levels, and the transfer of energy is not required to directly promote electrons to a specific upper level of the laser transition. Some approaches can be rather complex, but these often produce better-performing lasers. One frequently utilized approach excites an atom or molecule to a higher energy level than required, after which it drops to the upper laser level. Indirect excitation can be employed to excite atoms in a surrounding gas mixture, which then transfer their energy to the atoms or molecules responsible for producing the laser action.
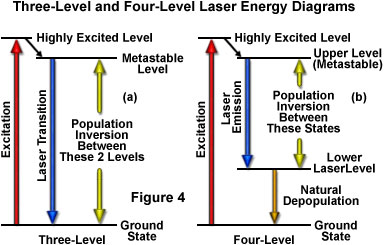
As previously discussed, the amount of time spent by an atom or molecule in an excited state is critical in determining whether it will be stimulated to emission and participate in a cascade of photons, or lose its energy through spontaneous emission. Excited states commonly have lifetimes of only nanoseconds before they release their energy by spontaneous emission, a period that is not lengthy enough to likely undergo stimulation by another photon. A critical requirement for laser action, therefore, is a longer-lived state that is suitable for the upper energy level. Such states do exist for certain materials, and are referred to as metastable states (see Figure 4). The average lifetime before spontaneous emission occurs for a metastable state is on the order of a microsecond to a millisecond, quite a lengthy period of time on the atomic timescale. With lifetimes this long, excited atoms and molecules can produce significant amounts of stimulated emission. Laser action is only possible if the population builds up faster than it decays in the upper energy level, maintaining a population larger than that of the lower level. The longer the spontaneous emission lifetime, the more suitable a molecule or atom is for laser applications.
The maser that Charles Townes demonstrated in advance of the first laser was significant because it required the creation of a population inversion in order to function, and therefore proved to many skeptical physicists that such an inversion could be produced. His system was a two-level maser, utilizing only the upper and lower energy levels. Townes employed a novel approach in his ammonia molecule system to produce the population inversion - a molecular beam technique that separated the excited ammonia molecules from ground-state molecules. The ground-state molecules were discarded, and the separated excited molecules constituted the required population inversion. Other, more efficient, means have now been developed for masers, and practical lasers require the utilization of three, four, or more energy levels.
The simplest functional energy-level structure for laser operation is a three-level system, which is illustrated in Figure 4(a). In this system, the ground state is the lower laser level, and a population inversion is created between this level and a higher-energy metastable state. Most of the atoms or molecules are initially excited to a short-lived high-energy state that is higher than the metastable level. From this state they quickly decay to the intermediate metastable level, which has a much longer lifetime than the higher energy state (often on the order of 1000 times longer). Because each atom's residence time in the metastable state is relatively long, the population tends to increase and leads to a population inversion between the metastable state and the lower ground state (which is continuously being depopulated to the highest level). Stimulated emission results from the fact that more atoms are available in the upper excited (metastable) state than in the lower state where absorption of light would most likely occur.
Although the three-level laser system works for all practical purposes, as exemplified by Maiman's first laser, a number of problems limit the effectiveness of this approach. The central problem occurs because the lower laser level is the ground level, which is the normal state for most atoms or molecules. In order to produce the population inversion, a majority of ground state electrons must be promoted to the highly excited energy level, requiring a significant input of external energy. In addition, the population inversion is difficult to sustain for an appreciable time, and therefore, three-level lasers must be operated in pulsed mode rather than continuously.
Lasers utilizing four or more energy levels avoid some of the problems mentioned above, and therefore are more commonly utilized. Figure 4(b) illustrates a four-level scenario. The energy level structure is similar to that in the three-level system, except that after the atoms drop from the highest level to the metastable upper state, they do not drop all the way to the ground state in a single step. Because the population inversion is not created between the ground state and the upper level, the number of atoms or molecules that must be elevated is dramatically reduced in this model. In a typical four-level laser system, if only one or two percent of the atoms or molecules reside in the lower laser level (which is above the ground state), then exciting only two to four percent of the total to the higher level will achieve the required population inversion. Another advantage of separating the lower laser level from the ground level is that the lower level atoms will naturally fall to the ground state. If the lower laser level has a lifetime that is much shorter than the upper level, atoms will decay to the ground level at a rate sufficient to avoid accumulation in the lower laser level. Many of the lasers designed under these constraints can be operated in a continuous mode to produce an uninterrupted beam.
Actual working lasers are usually far more complex than the models described above. The upper laser level is often not a single level, but a group of energy levels that enables the required excitation energy to vary over a wide range during operation. The lower level may also consist of multiple levels, and if closely spaced upper levels each decay to a different lower level, a single laser may be operated on multiple transitions, producing more than one wavelength. The helium-neon laser, for example, is most commonly utilized to emit a single red wavelength, but it can also be operated at other transitions to produce orange, yellow, green, and infrared radiation. Many other factors exist in the design of practical lasers, including the nature of the active media. Multiple gases or other combinations of molecular species are often employed to improve the efficiency of capturing and transferring the energy, or to assist in depopulating the lower laser level.
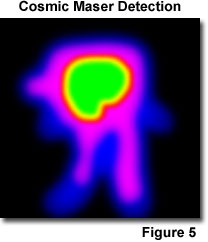
Before the landmark demonstration that masers and lasers could actually be produced, scientists had overlooked the fact that naturally occurring masers exist in outer space (Figure 5). Even after Einstein's prediction of stimulated emission, a majority of physicists believed that producing a population inversion was so difficult that it was unlikely to occur in nature. In effect, scientists apparently didn't seriously consider that matter could naturally exist in a state other than thermodynamic equilibrium. So-called cosmic masers include sources such as envelopes around red giant stars, comets, supernova remnants, and other star-forming molecular clouds. In the gas cloud surrounding a hot star, the radiation emitted from the star can excite the gas molecules to higher energy levels, which then decay to a metastable state. As long as a suitable lower laser level exists, a population inversion can occur that will result in laser action. Although the process is identical to man-made masers or lasers, and large amounts of energy can be radiated, emission of stellar laser or maser energy is not restricted to a beam. The radiation emitted by a cosmic maser travels outward in all directions just as the energy from any other interstellar hot gas cloud.
In addition to the creation of a population inversion, several other factors are required to amplify and concentrate light into a laser beam. Light from stimulated emission produced in a laser medium usually has a single wavelength, but must be extracted efficiently from the medium by some mechanism that includes amplification. This task is accomplished in a resonant cavity, which reflects some of the emission back into the laser medium and, through multiple interactions, builds or amplifies the light intensity. For example, after the initial stimulated emission, two photons having the same energy and phase are each likely to encounter excited atoms, which will subsequently emit even more photons having the same energy and phase. The number of photons produced by stimulated emission grows rapidly, and the increase is directly proportional to the distance the light travels in the laser medium.
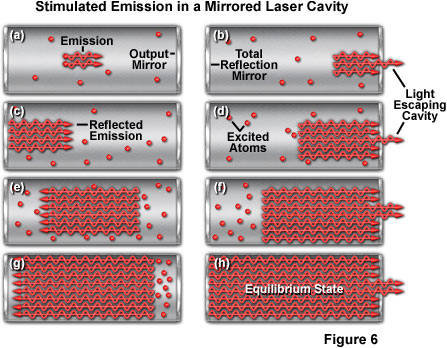
Presented in Figure 6 is an illustration of the gain, or amplification, that occurs with increased path length in the resonant cavity due to the mirrors at each end. Figure 6(a) shows the beginning of stimulated emission, which is amplified in Figure 6(b) through Figure 6(g) as the light is reflected from the mirrors positioned at the cavity ends. A portion of light passes through the partially reflecting mirror on the right-hand side of the cavity (Figures 6(b,d, and f)) during each pass. Finally, at the equilibrium state (Figure 6(h)), the cavity is saturated with stimulated emission.
The degree of amplification achieved in a laser, expressed by the term gain, refers to the amount of stimulated emission a photon can generate as it travels a given distance. For example, a gain of 1.5 per centimeter means that a photon generates 1.5 additional photons for every centimeter it travels. This results in an amplification factor that increases with the path length of the laser cavity. The actual gain is far more complex and depends upon fluctuations in the population distribution between the upper and lower laser energy levels, among other factors. The important point is that the amount of amplification increases sharply with the distance traveled through the laser medium.
In a laser constructed with a longitudinal resonant cavity, such as a ruby rod or a gas-filled tube, light traveling along the length of the laser medium generates far more stimulated emission than the light emitted perpendicular to the long axis of the cavity. Light emission is therefore concentrated along the length of the cavity even without the use of mirrors to confine its path to the lengthwise direction. Placing mirrors at opposite ends of a laser cavity enables the beam to travel back and forth, which results in increased amplification due to the longer path length through the medium. The multiple reflections also produce a narrowly focused beam (an important laser characteristic), because only photons traveling parallel to the cavity walls will be reflected from both mirrors. This arrangement is known as an oscillator, and is necessary because most laser materials have very low gain, and sufficient amplification can only be achieved with a long path length through the medium.
A majority of current lasers are designed with mirrors on both ends of the resonant cavity to increase the path that light takes through the laser medium. The emission intensity grows with each pass of light until it reaches an equilibrium level that is established by the cavity and mirror design. One cavity mirror reflects nearly the entire incident light, while the other (the output mirror) reflects some light and transmits a portion as the laser beam. In a laser that has low gain, the output mirror is chosen to transmit only a small fraction of the light (perhaps only a few percent), and to reflect the majority back into the cavity. At equilibrium, the laser power is higher inside the cavity than outside, and varies with the percentage of light transmitted through the output mirror. By increasing the transmittance of the output mirror, the difference in power between the inside and outside of the cavity can be reduced. However, as long as the output mirror reflects some portion of light back into the cavity, the power inside remains higher than in the emerging beam.
A common misconception about lasers results from the idea that all of the emitted light is reflected back and forth within the cavity until a critical intensity is reached, whereupon some "escapes" through the output mirror as a beam. In reality, the output mirror always transmits a constant fraction of the light as the beam, reflecting the rest back into the cavity. This function is important in allowing the laser to reach an equilibrium state, with the power levels both inside and outside the laser becoming constant.
Due to the fact that the light oscillates back and forth in a laser cavity, the phenomenon of resonance becomes a factor in the amplification of laser intensity. Depending upon the wavelength of stimulated emission and cavity length, the waves reflected from the end mirrors will either interfere constructively and be strongly amplified, or interfere destructively and cancel laser activity. Because the waves within the cavity are all coherent and in phase, they will remain in phase when reflected from a cavity mirror. The waves will also be in phase upon reaching the opposite mirror, provided the cavity length equals an integral number of wavelengths. Thus, after making one complete oscillation in the cavity, light waves have traveled a path length equal to twice the cavity length. If that distance is an integral multiple of the wavelength, the waves will all add in amplitude by constructive interference. When the cavity is not an exact multiple of the lasing wavelength, destructive interference will occur, destroying laser action. The following equation defines the resonance condition that must be met for strong amplification to occur in the laser cavity :
N • λ = 2 • (Cavity Length)
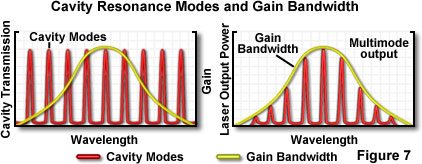
where N is an integer, and λ is the wavelength. The condition for resonance is not as critical as it might appear because actual laser transitions in the cavity are distributed over a range of wavelengths, termed the gain bandwidth. Wavelengths of light are extremely small compared to the length of a typical laser cavity, and in general, a complete roundtrip path through the cavity will be equivalent to several hundred thousand wavelengths of the light being amplified. Resonance is possible at each integral wavelength increment (for example 200,000, 200,001, 200,002, etc.), and because the corresponding wavelengths are very close, they fall within the gain bandwidth of the laser. Figure 7 illustrates a typical example in which several resonance values of N, referred to as longitudinal modes of the laser, fit within the gain bandwidth.
Laser beams have certain common characteristics, but also vary to a wide degree with respect to size, divergence, and light distribution across the beam diameter. These characteristics depend strongly upon the design of the laser cavity (resonator), and the optical system controlling the beam, both within the cavity and upon output. Although a laser may appear to produce a uniform bright spot of light when projected onto a surface, if the light intensity is measured at different points within a cross section of the beam, it will be found to vary in intensity. Resonator design also affects beam divergence, a measure of beam spreading as distance from the laser increases. The beam divergence angle is an important factor in calculating the beam diameter at a given distance.
In much of the previous discussion, the assumption has been that the mirrors at either end of a laser resonator cavity are planar, or flat. Conceptually this is the simplest configuration, but in practice it can be very difficult to accomplish. If the two mirrors are not precisely aligned, excessive light losses will occur that may cause the laser to stop operating. Even a misalignment of a fractional degree, after several successive reflections, can result in significant light losses from the sides of the cavity. If one or both of the mirrors have a curved surface, the light losses due to misalignment can be reduced or eliminated. Because of the focusing properties of the curved mirror, light is confined to the cavity even if the mirrors are not precisely aligned, or if the light is not emitted exactly along the cavity axis. There are a number of design variations that employ different combinations of plane and curved mirrors to ensure that the light is always focused back toward the opposite mirror. A configuration of this type is called a stable resonator because light that is reflected from one mirror to the other will continue to oscillate indefinitely if there are no other losses.
In a laser medium that has low gain, a stable resonator is very important in maximizing the use of the stimulated emission. In a high-gain laser, low-level losses from the sides of the cavity are not critical. In fact, certain unstable resonator designs may be preferred because they often have the advantage of collecting energy from a larger volume within the laser medium, even though they allow light loss. Mirrors in high-gain lasers are often more transparent than those in laser systems having lower gain, so that a given light ray may only travel once through the cavity before emerging in the beam. Therefore, alignment of the mirrors is not as critical as in a low-gain design, where high reflectivity of the output mirror causes the light to be reflected many times before emerging.
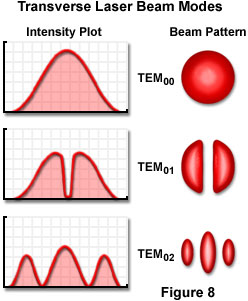
The laser cavity length and the wavelength of the light interact to produce longitudinal modes of energy distribution in the beam, but the resonator design is a key factor in determining the intensity distribution across the width of the beam, and the rate at which the beam diverges. The intensity across the beam is determined by the transverse mode of the beam. The possible distributions in beam intensity are limited by certain so-called boundary conditions, but usually a beam exhibits one, two, or more peaks in the center, with zero intensity at the edges. The various modes are designated as TEM(mn) modes, referring to Transverse, Electric, and Magnetic modes, respectively, where m and n are integers. The integers indicate the number of minima, or zero-intensity points, between the edges of the beam in two perpendicular directions (E-mode for the first, and M-mode, the second).
A typical laser beam is brightest in the center and drops off in intensity toward the edges. This represents the simplest first-order mode, is designated TEM(00), and has an intensity profile across the beam that follows a Gaussian function. Figure 8 illustrates several of the many TEM(mn) modes that are possible. Although some stable-resonator lasers, especially ones designed for maximum output power, operate in one or more of the higher-order modes, it is usually desirable to suppress these oscillations. The first-order mode can be obtained readily in stable-resonator low-gain lasers, and is the preferred mode since beam spreading due to diffraction can approach a theoretical minimum value.
Diffraction plays an important role in determining the size of laser spot that can be projected to a given distance. The oscillation of the beam in the resonator cavity produces a narrow beam that subsequently diverges at some angle depending on the resonator design, the size of the output aperture, and resulting diffraction effects on the beam. Diffraction is usually described as a beam-spreading effect that results from the formation of diffraction rings (termed Airy rings) that surround a beam when the light waves have passed through a small opening. These diffraction phenomena impose a limit on the minimum diameter of a light point after passing through an optical system. For a laser, the beam emerging from the output mirror can be thought of as the opening or aperture, and the diffraction effects on the beam by the mirror will limit the minimum divergence and spot size of the beam. For beams in TEM(00) mode, diffraction is usually the limiting factor in beam divergence. The nominal value of the beam divergence is given by the simple relationship:
Divergence (in radians) = Constant • Wavelength / Beam Diameter
If the laser beam passes through an optical system, the appropriate diameter value in the above equation is that of the last element through which the beam passes. The constant depends on the intensity distribution in the beam, and is very close to unity in value. The relationship clearly demonstrates that beam divergence increases with wavelength, and decreases as beam (or output lens) diameter increases. In other words, a smaller diameter beam will suffer more divergence and greater spread with distance than a larger beam.
The values of beam divergence for a given laser can have tremendous practical significance. Helium-neon and semiconductor lasers have become standard tools in field surveying. In laser ranging, a fast laser pulse is sent to a corner reflector at the location to be mapped, and the delay in return of the pulse is precisely measured to obtain the distance from the laser location. Over the customary short distances, beam divergence is not a significant issue, but for lengthy distance measurements, excessive divergence can reduce the reflected beam intensity and hamper detection. United States astronauts on the Apollo 11 and Apollo 14 missions placed corner reflectors on the moon that were employed to reflect light from a powerful pulsed ruby laser at the MacDonald Observatory in Texas. Even though the beam had spread to a radius of 3 kilometers at the moon's surface, reflected light still had enough intensity to be detected on Earth. The distance from the moon to the Texas observatory was measured to within 15 centimeters in this experiment, but since the 1980s, technological advances have increased the accuracy to a value of less than 2 centimeters. Current efforts are underway that employ powerful telescopes to transmit and receive light pulses using several reflectors on the moon to further reduce the error, perhaps to as low as 1 millimeter.
Because the mechanism of producing laser action involves raising atoms or molecules to a high excitation state in order to produce the required population inversion, it is obvious that some form of energy must be expended into the laser system. Photons can be used to provide the necessary energy in a process known as optical pumping. By illuminating the laser material with light of an appropriate wavelength, the emitting atom or molecule can be raised to the upper energy level, from where it then drops to the metastable level and subsequently becomes stimulated to emit light. Fortunately, in most lasers, the light used for pumping does not have specific wavelength requirements, primarily because the laser may have multiple upper levels that can all decay to the metastable level. Therefore, an inexpensive light source emitting a broad range of wavelengths, such as an incandescent lamp or flash tube, can often be used to optically pump lasers. An important factor that limits laser efficiency is that the pump light photons must have higher energy (or the equivalent shorter wavelength) than the laser light.
Electrical pumping is another mechanism of excitation that is commonly utilized in gas and semiconductor lasers. In a gas laser, an electrical current flowing through the gas excites the atoms and molecules into the upper energy level necessary to begin the decay, or decay series, that produces the laser emission. Some gas lasers pass a constant current through the gas to produce continuous output, while others use pulses of current to produce pulsed laser output. Some high-powered lasers even use electron beams directed into the gas for excitation.
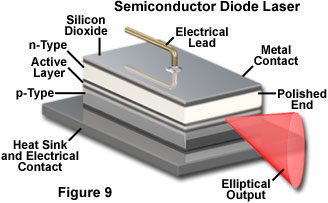
Semiconductor lasers operate in a very different fashion, but also rely on electrical currents to produce the necessary population inversion. In these devices the inversion is produced between populations of current carriers (electrons and electron-hole pairs) in the plane of the junction between dissimilar regions of the semiconductor. Light emission in a semiconductor laser is concentrated in the junction plane by feedback from the cleaved ends of the crystal (Figure 9). The chip material has a high refractive index, and reflects enough light back into the crystal to achieve gain. The cleaved face can also be polished to control the reflectivity. Typically one end of the crystal is coated with a reflective material so that emission only occurs from a single end, as illustrated in Figure 9. Much lower electrical potential and current is required in semiconductor lasers as compared to gas lasers.
Other means of energy transfer are less commonly employed to power laser transitions. Nuclear or chemical reactions may be utilized to generate excited species in some lasers. Gas lasers may use a combination of different gases to carry out the laser process. In the helium-neon laser, the helium atoms capture energy from the gas discharge that is caused by an electrical input, which is then transferred to very close energy levels that exist in the neon gas. The laser transition subsequently occurs in the neon gas to produce the laser emission.
Lasers are inherently inefficient. Energy must be supplied to the laser, and some is lost in the conversion to more highly ordered energy in the form of laser light. As discussed above, for an optically pumped laser, the laser output is always longer in wavelength than the pump light. Other energy losses occur during energy level changes that take place in three-level and four-level lasers. Following the initial excitation to the upper level, the laser transition itself may only release part of that energy, especially with the rest being lost to other processes. In some systems, with a high-energy laser transition, a great deal of energy must be expended just to raise the laser species to the appropriate level, far above the ground state. Excitation, whether by electrical or optical means, is not 100 percent efficient - the energy is never fully absorbed by the laser medium. All of these major factors, and some minor ones not mentioned, seriously limit the overall efficiency of lasers. Although the most efficient semiconductor lasers and some gas lasers can convert almost 10 percent of the input energy into laser light, the typical laser has an overall efficiency of 1 percent or less.
In a few decades since the 1960s, the laser has gone from being a science fiction fantasy, to a laboratory research curiosity, to an expensive but valuable tool in esoteric scientific applications, to its current role as an integral part of everyday tasks as mundane as reading grocery prices or measuring a room for wallpaper. Any substantial list of the major technological achievements of the twentieth century would include the laser near the top. The pervasiveness of the laser in all areas of current life can be best appreciated by the range of applications that utilize laser technology. At the spectacular end of this range are military applications, which include using lasers as weapons to possibly defend against missile attack. At the other end are daily activities such as playing music on compact disks and printing or copying paper documents. Laser pointers that once cost hundreds of dollars are sold as inexpensive key chain accessories, and even carpenter's levels and simple measuring devices incorporate lasers.
In between the fantastic and the ordinary, lasers are widely employed in medical treatment and surgery, and in cutting and welding everything from fabric used for clothing to steel, rubber, and plastic used in the manufacture of automobiles and appliances. The heat from lasers is utilized in spot welding metals, and in medical procedures as delicate as reattaching a retina that has become detached in the human eye. Other highly precise medical procedures such as repairing vascular damage and cutting and fusing tissue are routinely accomplished using lasers. A large part of worldwide telephone communications are conducted by sending pulsed laser signals over miles of fiber optic cable, and cultural artifacts, such as ancient paintings, are often evaluated for flaws and restored with the help of lasers. Along with the computer, the integrated circuit, and the satellite, laser technology seems destined to grow in importance in our everyday lives in ways not dreamed of just a few short years ago.
Sorry, this page is not
available in your country.



