Focus Depth and Spherical Aberration

Optical Aberrations - Focus Depth and Spherical Aberration - Java Tutorial

The image of each point source seen in the microscope is formed by the constructive and destructive interference of light waves that leave the rear aperture of an objective in a finite-tube microscope or the tube lens (instead of the objective rear aperture) in an infinity-corrected microscope. Aberration-free optical systems produce a symmetrical diffraction image of a point source at varying focal levels, as discussed in our Axial Resolution and Depth of Field interactive Java tutorial.

The tutorial initializes to display an aberration-free meridional section derived from the computed point spread function (PSF) of a point source of light located at a depth (d) in the specimen layer having a refractive index of 1.33 (typically found in aqueous solutions), and imaged with a virtual microscope objective. The Specimen Layer Depth slider is utilized to transform the point spread function through a series of specimen depths.

The lateral resolution for an Airy diffraction pattern generated by a point light source is defined within a single plane of focus at the intermediate image position in an optical microscope. When the aperture function of an objective is non-uniform, or in the case of spherical aberration, the wavefront leaving the lens is no longer spherical with a center positioned at the point of focus in the image plane. Instead, the wavefront is distorted and departs from ideal behavior in a manner that is dependent upon the nature of the aberration and/or image filters and conditions that are present in the optical system. At the intermediate image plane, the point spread function yields an asymmetrical distribution where the intensity ratio between the central peak and surrounding rings is shifted with the latter becoming far more prominent. This concept is explored with interactive tutorials in the section on Spherical Aberration in microscope objectives.

In fact, for lenses afflicted with spherical aberration, the diffraction image of a point source extends periodically above and below the intermediate image plane into a three-dimensional pattern that expands and spreads out asymmetrically from the center along the optical axis. Cross-sections taken along the optical axis of the microscope near the focal plane using a high numerical aperture objective with spherical aberration are illustrated in Figure 1. It is apparent that diffraction images are not symmetric above and below exact focus (the paraxial focal point; Figure 1). The asymmetry of the sectioned diffraction rings can be seen especially clearly when the image of a point source is focused rapidly above and below the paraxial focal point. This concept is utilized by lens inspectors and practiced microscopists to diagnose the presence of even slight amounts of spherical and other aberrations.

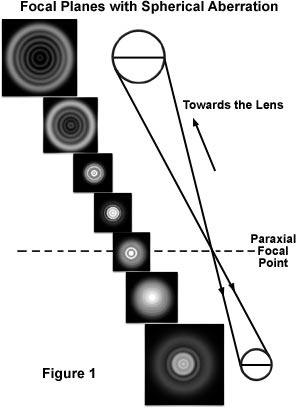
It is not a simple matter to determine which is the level that produces the "best focus", and it is easy to misinterpret the focal levels. The result often leads to erroneous conclusions about the actual specimen structure giving rise to the image, including a sense of false high resolution. In the presence of spherical aberration and/or astigmatism, maximum contrast may not be an indication of desirable focus, an error that can be compounded with periodic specimens. Furthermore, distortion introduced by spherical aberration may not only affect image quality and fidelity, which affect interpretation and measurement of the specimen, but also the efficiency of confocal and other imaging modes in which the microscope optics are used to reduce the image to obtain a diffraction-limited illuminating point.

For specimens mounted in Canada balsam or similar mounting media with a refractive index that approximates the coverslip, the thickness of the coverslip is not of primary concern when using oil immersion objectives. However, for specimens that are bathed or mounted in physiological saline solutions or other aqueous media, the refractive index of the media is significantly different from that of the coverslip and spherical aberration can become significant. Figure 2 illustrates the changes in size and intensity distribution through the image point (in the intermediate image focal plane) with increasing penetration into a specimen mounted in aqueous medium with an immersion oil objective.

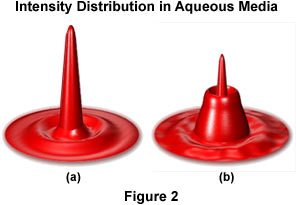
In Figure 2, the change in intensity distribution, illustrated as computed point spread functions at the intermediate image plane, is shown with increasing penetration into an aqueous medium with a plan apochromat oil immersion objective. Figure 2(a) illustrates the point spread function at a penetration depth of zero microns, while Figure 2(b) shows the distribution at a depth of four microns. It should be noted that peak intensity in these functions has been normalized. In practice, the intensity would dramatically decrease as the base of the intensity plot widens. At the water-coverslip interface, spherical aberration is generated, which shifts the focus of peripheral rays above the optimal focus of paraxial rays. The effect of this induced spherical aberration on the image point should be considered, because the optical assumptions used to calculate objective lenses for aberration correction by microscope manufacturers no longer hold.

To compensate for the behavior of oil immersion objectives in aqueous media, manufacturers have introduced well-corrected water immersion objective lenses. Although these objectives do not provide the high numerical apertures available with their oil immersion counterparts, they do overcome aberration induced by refractive index mismatches with specimens bathed in aqueous media. With the best objectives, it is now possible to focus through approximately 200 micrometers of aqueous media and still retain excellent optical correction.

Spherical aberration can also arise through modified aperture functions, especially when employing contrast enhancing techniques that place additional optical components into the microscope light path. An excellent example is the accidental mismatch of differential interference contrast (DIC) prisms where the intended shear and numerical aperture of the prism does not match that of the objective. Additional problems can arise from the presence of stress birefringence in the substage condenser, the microscope slide (and/or other specimen container), or one of the objective lenses. Alignment problems in the microscope optical pathway can also modify aperture performance as can the need to focus through layers of refractile tissue or the absence of rectification in polarization microscopy. Inspection of the optical integrity through conoscopic observation (at the objective rear focal plane), combined with routine focusing above and below the plane of interest, can often reveal the sources of nonuniform apertures that affect or degrade image quality.

Modern microscope optical components are generally corrected for aberrations to meet a rigid set of specifications for the particular class of optics. However, this does not circumvent damage to objectives or other microscope lenses during use or the application of these components in ways that are not appropriate. For critical photomicrography, microscopists must pay particular attention to the alignment and integrity of all microscope components including the objective/condenser combination, light sources, coverslip thickness, immersion media, tube length, and overall cleanliness of glass surfaces. Tiny water or oil droplets, smeared films, or air bubbles in immersion oil, as well as nonuniform illumination of the condenser or objective aperture, can distort the wavefront of light emanating from the specimen and corrupt even the best, well-corrected microscope optics.