Les représentations graphiques de la FTM procurent une méthode quantitative et standardisée pour comparer les performances de différents objectifs. Elles constituent donc un outil de mesure très utile pour la conception d’instruments optiques.
Pour ceux qui ne connaissent pas ce sigle, « FTM » signifie « fonction de transfert de modulation ». Ce paramètre mesure la capacité d’un objectif à transférer le contraste d’un échantillon sur une image en utilisant la fréquence spatiale (résolution). La fréquence spatiale indique le nombre de paires de lignes (c’est-à-dire une ligne noire et une ligne blanche) par millimètre (pl/mm). Vous pouvez en voir des exemples à la figure 1.
Les composants optiques de haute qualité transfèrent plus de contraste à des fréquences plus élevées (c’est-à-dire à une résolution plus élevée). Même si la fréquence (résolution) est élevée, un faible contraste vous empêchera de voir clairement les détails de l’échantillon. En d’autres termes, pour la qualité de l’image, le contraste est tout aussi important que la résolution. Dans une représentation graphique de la FTM, le contraste de l’objectif est représenté en fonction de la fréquence. Les courbes du graphique vous permettent de comparer visuellement les différences de performances entre les objectifs.

Figure 1. Exemples de différentes fréquences spatiales (résolution).
Les ingénieurs demandent les représentations graphiques de la FTM aux fabricants d’objectifs lors du processus de conception. Par exemple, nous avons récemment reçu de nombreuses demandes de représentations graphiques de la FTM optique de la part d’ingénieurs responsables de concevoir des analyseurs de cellules, des séquenceurs d’ADN, des scanners de lames ou des équipements d’inspection industrielle. Pour aider nos clients à concevoir le meilleur système optique, cet article explique les différentes façons d’utiliser les représentations graphiques de la FTM.
Exemple de représentation graphique de la FTM (et comment la lire)
La figure 2 ci-dessous montre un exemple de représentation graphique de la FTM. Le champ de vision est fixe, l’axe horizontal indique la fréquence spatiale et l’axe vertical indique le contraste. Le graphique indique qu’un contraste de 50 % peut être obtenu avec cet objectif à une fréquence spatiale de 30 pl/mm.
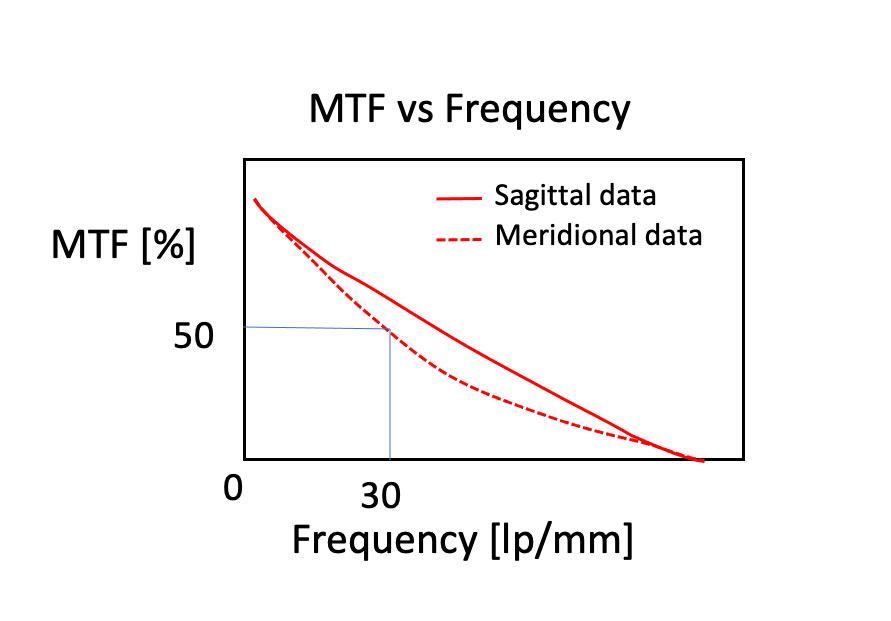
Figure 2. Exemple de graphique de la FTM représentant le contraste (FTM) en fonction de la fréquence spatiale
Une représentation graphique de la FTM peut également prendre la forme de courbes dans les directions sagittale et méridienne. Ces courbes illustrent la manière dont le contraste change en fonction de la distance à partir du centre de l’image :
- La courbe sagittale indique les performances dans la direction radiale (du centre vers le coin de l’image).
- La courbe méridienne indique les performances dans la direction concentrique (circulaire).
Notez que pour la plupart des objectifs, le contraste est généralement plus fort au centre du champ de vision que sur les bords. Le contraste dans les directions sagittale et méridienne change en raison de l’influence des aberrations hors axe (c’est-à-dire des erreurs optiques à différents points du champ). Le coma et l’astigmatisme sont de bons exemples.
En général, des caractéristiques sagittales et méridiennes similaires créent une image plus uniforme. Si les courbes sagittale et méridienne sont proches l’une de l’autre sur une représentation graphique de la FTM, les images présenteront des performances plus uniformes sur l’axe X (horizontal) et l’axe Y (vertical). Un écart entre les deux courbes indique généralement une image inégale avec des aberrations. Idéalement, on souhaite que les courbes soient proches l’une de l’autre pour obtenir des performances d’image plus uniformes.
Cinq façons d’utiliser les représentations graphiques de la FTM pour la conception d’instruments optiques
Lors de la conception d’un instrument optique, les ingénieurs doivent optimiser de nombreux composants pour construire un système final qui satisfait à tous les critères requis. Par exemple, le système optique d’un appareil d’imagerie microscopique comprend un objectif, une lentille de tube et un adaptateur de caméra. Les représentations graphiques de la FTM constituent un moyen objectif (sans mauvais jeu de mots) de caractériser les performances des objectifs et des autres composants optiques utilisés dans le système.
1. Comparaison des performances optiques avec la limite de diffraction idéale
La limite de diffraction indique la limite absolue de la résolution dans un système optique. En comparant la valeur limite de diffraction avec la FTM du système de lentilles, vous pouvez évaluer à quel point les performances du système de lentilles se rapprochent de la valeur théorique.
Une représentation graphique de la FTM peut vous montrer en un coup d’œil la différence entre le système optique idéal et le système conçu. Par exemple, supposons que vous compariez les FTM de deux systèmes optiques (figure 3). Vous pouvez constater que le système 1 a des performances supérieures à celles du système 2, car il est plus proche de la valeur limite de diffraction.
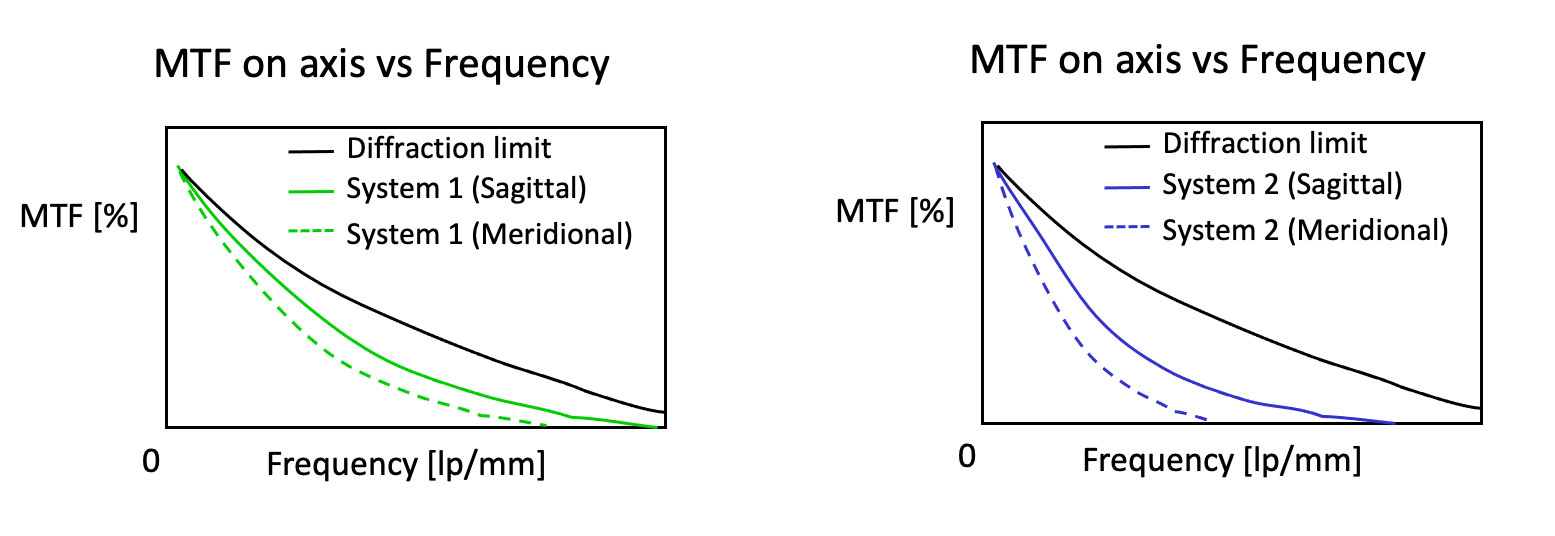
Figure 3. Courbes de la FTM de deux systèmes optiques.
La comparaison côte à côte permet de voir quel système se rapproche le plus de la limite de diffraction.
2. Comparaison des performances de différents objectifs
La FTM constitue un bon indicateur si vous souhaitez comparer les performances de différents objectifs, car elle indique quel objectif assure le contraste le plus fort à une certaine fréquence spatiale. Comme nous l’avons mentionné précédemment, un contraste plus fort entraînera de meilleures performances d’image. Les représentations graphiques de la FTM facilitent la comparaison du contraste des composants optiques puisque vous pouvez voir quelle courbe de la FTM est la plus haute.
La représentation graphique de la FTM ci-dessous (figure 4) en donne un exemple. Vous pouvez voir que les courbes de la FTM indiquent que les performances de l’objectif A sont meilleures que celles de l’objectif B puisqu’elles sont plus hautes. Ces informations visuelles peuvent vous aider à sélectionner le bon objectif pour la conception de votre système.
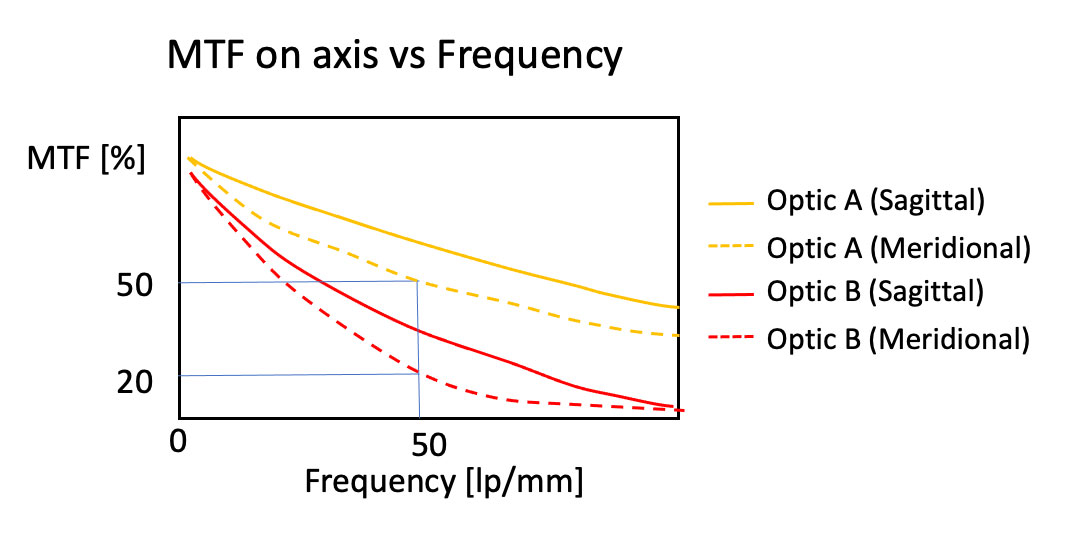
Figure 4. Courbes de la FTM de deux objectifs différents. La courbe de l’objectif A est plus haute que
celle de l’objectif B, ce qui indique que l’objectif A a de meilleures performances optiques.
3. Détermination de la FTM à différentes positions de mise au point dans le champ de vision
Une représentation graphique de la FTM peut également vous montrer à quel point les composants optiques sont sensibles à la défocalisation en représentant la différence de FTM entre les positions de mise au point dans l’axe et hors axe :
- La position de mise au point dans l’axe désigne le centre du champ de vision qui forme une image bien nette.
- La position de mise au point hors axe désigne une position à la périphérie du champ de vision.
Examinons la figure 5 ci-dessous à titre d’exemple. La FTM à la position de mise au point dans l’axe est de 60 %, alors que la FTM à la position de mise au point hors axe est de 40 %. On peut donc déduire qu’en position hors axe, la FTM est réduite de 20 %. Les valeurs acceptables varient selon l’application. Si les valeurs ne sont pas acceptables, envisagez de modifier la conception du système ou d’utiliser d’autres composants optiques.
Idéalement, pour produire une image nette, la courbe de la FTM pour la position hors axe doit être aussi proche que possible de celle pour la position dans l’axe. Un écart entre les courbes des positions dans l’axe et hors axe (voir la figure 5 ci-dessous) indique des problèmes de défocalisation causés par des aberrations.
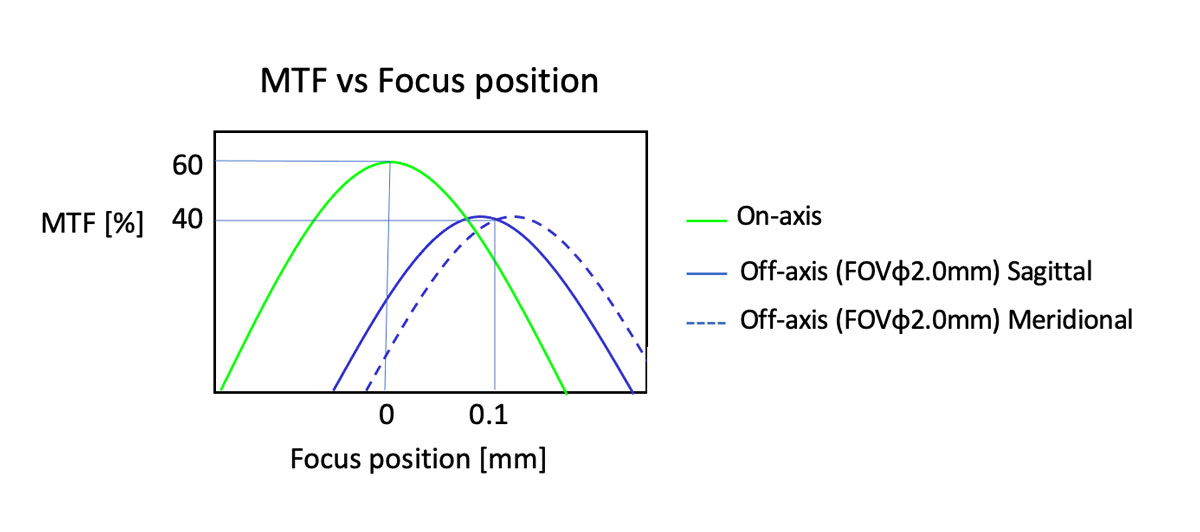
Figure 5. Courbes de la FTM à différentes positions de mise au point (pic des courbes) dans le champ de vision.
L’écart entre les courbes des positions dans l’axe et hors axe indique des problèmes de défocalisation.
4. Détermination de la hauteur idéale de l’image pour le capteur
La hauteur de l’image est la distance entre le centre et le bord de l’image. Une représentation graphique de la FTM vous permet de déterminer visuellement la hauteur idéale de l’image à la position du capteur du système optique. Vous pouvez également vérifier la différence entre les performances de la position du capteur dans l’axe et de la position du capteur hors axe.
La figure 6 ci-dessous en montre un exemple. Jetez un œil à la FTM aux positions centrale et hors axe du capteur. La FTM en position centrale est de 70 %. La FTM en direction méridienne à 5 mm du centre est de 50 %. Normalement, plus le capteur s’éloigne du centre, plus la FTM se dégrade en raison des effets des aberrations hors axe. Dans cet exemple, la FTM en direction méridienne devient 20 % à 10 mm du centre. Pour des performances optimales, assurez-vous de vérifier la FTM à la hauteur d’image requise pour l’application lors de la conception de votre système.
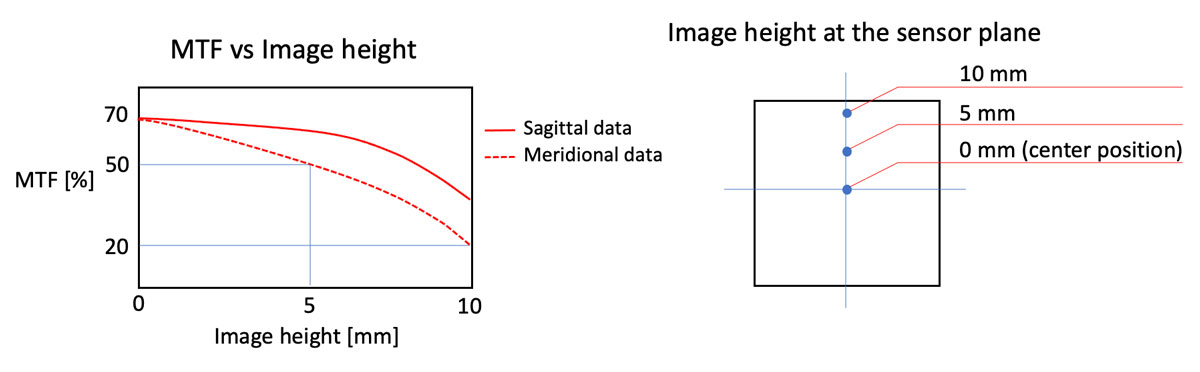
Figure 6. Représentation graphique de la FTM pour différentes hauteurs d’image.
La FTM se dégrade à mesure que le capteur s’éloigne du centre.
5. Comparaison de la FTM pour plusieurs composants optiques d’un système
Les représentations graphiques de la FTM sont aussi utiles pour vérifier les FTM de différents composants optiques au sein d’un même système, comme un objectif et une lentille de tube. Cela vous permet de voir s’il y a une dégradation de la FTM causée par l’un des composants optiques. Avec ces informations, vous pouvez modifier les composants pour obtenir les performances optimales nécessaires pour le système. Par exemple, il est possible de calculer la FTM d’un objectif seul, d’une lentille de tube seule et d’un système optique qui combine un objectif et une lentille de tube.
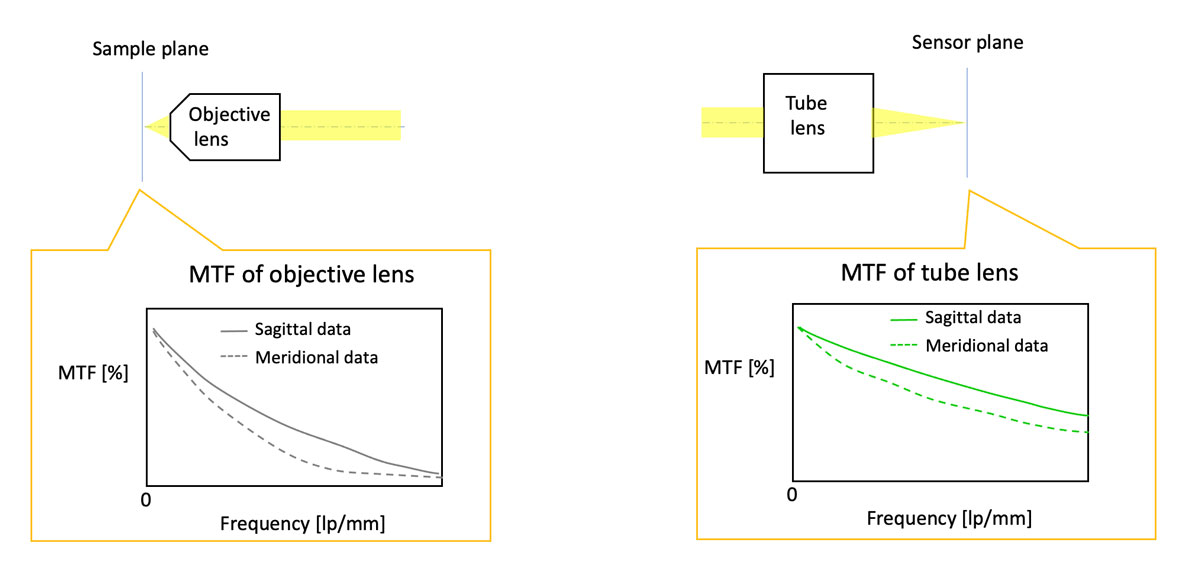
Figure 7. Représentations graphiques de la FTM pour un objectif (à gauche) et une lentille de tube (à droite)
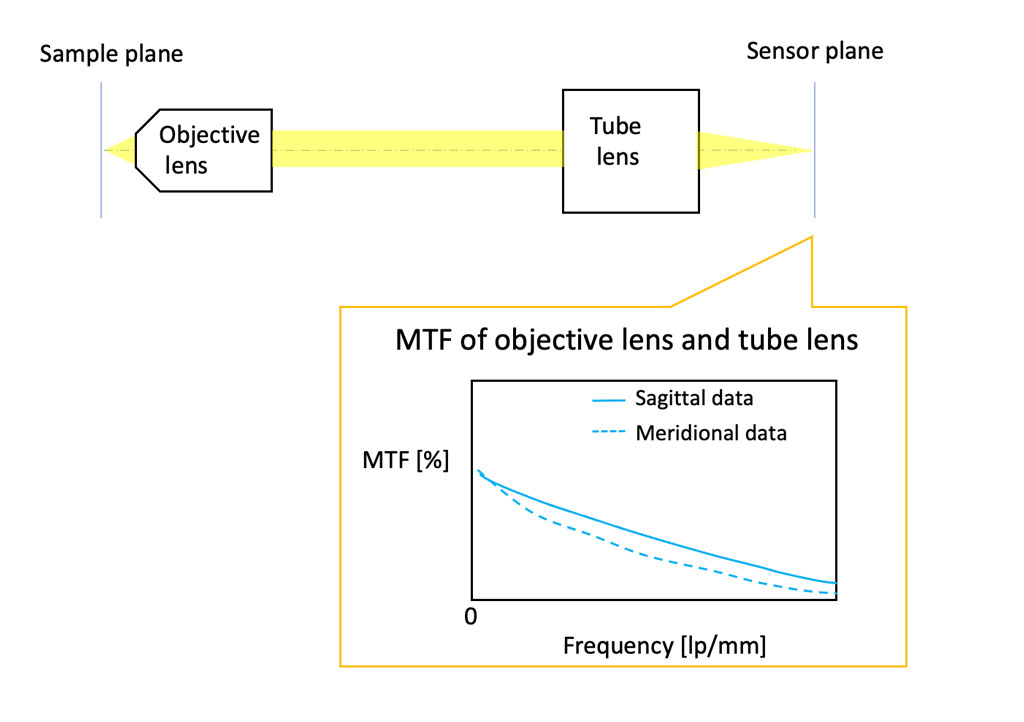
Figure 8. Graphique de la FTM représentant les performances optiques combinées de l’objectif et de la lentille de tube
Éléments à prendre en compte pour l’utilisation des représentations graphiques de la FTM et lectures complémentaires
La façon dont vous utilisez les représentations graphiques de la FTM dépend en fin de compte de la finalité de votre instrument. Par exemple, la FTM peut être calculée pour une longueur d’onde particulière (lumière monochromatique) ou pour de la lumière blanche. Les applications laser pour l’imagerie de fluorescence ou multiphotonique peuvent nécessiter des données de FTM pour des longueurs d’onde particulières. Les applications d’imagerie génériques peuvent nécessiter des données de FTM pour la lumière blanche.
Le capteur est un autre élément important à prendre en compte en ce qui concerne la FTM. Notez que lors de la caractérisation d’un système optique au moyen de la FTM, il est nécessaire de choisir un capteur ayant un pas de pixel et une fréquence de Nyquist optimaux. Pour plus de détails, lisez notre article technique, Éléments à prendre en compte lors du choix d’une caméra pour microscope.
Vous avez des questions sur les représentations graphiques et les données de la FTM ? N’hésitez pas à contacter nos experts pour obtenir des conseils.
Remarque : Evident communique les données de FTM à condition de signer un accord de non-divulgation (NDA). Ces données peuvent être utilisées pour créer un système optique offrant des performances optiques supérieures.
Contenu connexe
Comment miniaturiser un système optique pour fabriquer un appareil d’imagerie compact
Qu’est-ce que la fonction de transfert de modulation ?
Comment utiliser l’outil « Trouver le bon objectif » en cinq étapes faciles

