After deconvolution algorithms have been applied, the restored image may include apparent artifacts such as striping, ringing, or discontinuous cytoskeletal staining. In some instances, these problems are related to data representation and will not occur with a different algorithm or software package. The artifacts can also occur when processing parameters are not correctly configured for the raw image. Finally, artifacts are often not caused by computation, but by histology, optical misalignment, or electronic noise. When attempting to diagnose the source of an artifact, the first step is to carefully compare the raw image with the deconvolved image.
If the artifact is visible in the raw image, then it must be caused by factors upstream from deconvolution. By adjusting the contrast and brightness of the raw image, some artifacts can be revealed that are not apparent upon first glance. If the artifact is not present or is undetectable in the raw image, then some aspect of deconvolution is implicated. In the latter case, it may be useful to compare the results of deconvolution by a variety of algorithms (for example, an inverse filter versus a constrained iterative algorithm).
Point Spread Function Considerations
The quality of the point spread function (PSF) is critical to the performance of a deconvolution algorithm and should be paid very close scrutiny. A noisy, aberrated, or improperly scaled point spread function will have a disproportionate effect on the results of deconvolution. This is especially true for the iterative techniques because the point spread function is repeatedly applied to the calculations. In all cases, the distribution and extent of blurred light in the raw image must match the point spread function. If a mismatched point spread function is utilized, then artifacts may result or restoration quality may diminish.
In many commercial deconvolution software packages, the user can choose either a theoretical or an empirical point spread function for image restoration. In general, results are better if an empirical point spread function is employed, and there are several important reasons not to preferentially use a theoretical point spread function. First, although good theoretical models for the point spread function exist, they are not perfect models, and an empirical point spread function contains information not available in theoretical models. Second, the theoretical point spread function available in commercial software packages generally assumes perfect axial and rotational symmetry, which means it may not correctly fit the distribution of blur in the raw image. This problem is most serious at high resolution (for example, with objectives having numerical apertures ranging between 1.2 and 1.4), where small manufacturing variations in the lens assembly or optical coatings can induce minor aberrations in the symmetry of the point spread function. A theoretical point spread function does not reflect these lens-specific variations and yields inferior deconvolution results. Furthermore, an empirical point spread function can be helpful in selecting the proper objective for deconvolution analysis.
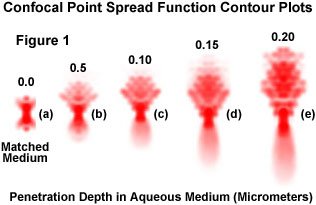
Presented in Figure 1 are a series of theoretically generated contour plots of confocal point spread functions at progressively deeper nominal focus positions into a water medium. The utilization of an oil immersion objective is assumed, and the significant axial spread of the point spread function results from the mismatch in refractive index between the immersion oil and water, which increases with focus depth. The complexity of the aberration in point spread function attributable to just this one variable in the theoretically modeled plots illustrates why empirical measurement of the point spread function is a preferable means of accurately accounting for aberrations that might affect deconvolution results. Figure 1(a) illustrates the unaberrated confocal PSF in matched-index media, with no aberrations present. The axial extent of the point spread function clearly increases as the focus position is changed to greater depth along the z-axis (Figure 1(b) through 1(e)), and the PSFs are shifted toward the objective.
Aberrations that are difficult to detect when examining complicated specimens become very clear when examining the point spread function generated from a single fluorescent bead. Therefore, before purchasing a costly new objective, it is recommended that point spread functions from several objectives be acquired and compared to help select the system with the most ideal point spread function. Another benefit of the empirical point spread function is that it enables the microscopist to measure the performance of the imaging system. Many potential problems that may occur during an experiment, such as stage drift, lamp flicker, camera noise, refractive index mismatches, and temperature fluctuations will also occur during point spread function acquisition and are more easily discernable. Therefore, aberrations in the empirical point spread function suggest ways to improve the quality of images captured in the microscope.
When acquiring an empirical point spread function, care must be taken to match aberrations appearing in the raw image. Ideally, both the raw image and the point spread function should be free of aberration, but this is not always possible. If major aberrations are present in the raw image, then they should (if possible) be matched by aberrations in the point spread function. Otherwise, the deconvolved image may contain errors or be poorly restored. In addition, if the point spread function is noisy, then substantial noise will appear in the deconvolved image. To reduce noise and eliminate minor aberrations, many software packages radially average the point spread function or average the images of several fluorescent beads to create a smoother point spread function. Another feature of many commercial software packages is that they automatically interpolate the sampling interval of the point spread function to match the sampling interval of the raw image. If this not the case, the point spread function and raw image must be acquired at the same sampling interval.

When utilizing a theoretical point spread function, the point spread function parameters must be set appropriately. These parameters include imaging modality, numerical aperture, emitted light wavelength, pixel size, and z-step size, and they can dramatically affect the size and shape of the resulting point spread function. In general, point spread function size increases with increasing wavelength and with decreasing numerical aperture. The pixel size and z-step parameters are utilized for scaling the point spread function with respect to the raw image.
If the size and shape of the theoretical point spread function are not appropriate to the raw image, then artifacts can result for a variety of reasons. First, the algorithm interprets the sampling interval of the image in terms of the point spread function size. Second, the point spread function determines the size and shape of the volume from which blurred light is reassigned. If the volume does not correspond to the true distribution of blur in the image, then artifacts can be introduced. This error can occur if there is mis-scaling or aberration in the point spread function. It can also result if the "real point spread function" of the image has an aberration that is not matched by the point spread function generated by the algorithm.
In some cases, when using a theoretical point spread function, better results may be obtained when the point spread function is apparently too large. A possible explanation is that the real point spread function of the raw image is larger than expected. This might occur because of a refractive index mismatch, which induces spherical aberration and alters z-axis scaling. Both phenomena widen the real point spread function in the z direction, making it larger and thereby lowering the effective numerical aperture of the objective. If this case is suspected, the investigator should attempt to subtract a small increment (for instance, 0.05) from the numerical aperture of the theoretical point spread function. In some software packages, a similar result is obtained by setting the z-step size of the point spread function to be smaller than the actual z-step utilized in acquiring the raw image.
Normally, the z-step size of the point spread function should always be identical to the z-step of the raw image. This caution ensures that the scaling of the point spread function is appropriate to the imaging conditions. With an empirical point spread function, however, it may be possible to acquire a point spread function at finer z-resolution than the raw image. It should be mentioned that this trick works only if the software can interpolate the sampling interval of the image and make it correspond to the point spread function.
Currently, most commercially available deconvolution software packages assume that the point spread function is constant for all points in the object, a property known as spatial invariance. Microscope optics generally meet this assumption, but other issues such as refractive index gradients in the specimen material or a mismatch of immersion and mounting media can induce spatial variations in the point spread function, especially in thick specimens. At present, all commercial software packages assume spatial invariance, but in the future (due to rapidly increasing computer processing speeds) it may be feasible to vary the point spread function through the image. It may also become possible to correct spatial variations in the point spread function by employing a transmitted light image to map refractive index gradients in the specimen and adjust the point spread function accordingly.
Spherical Aberration
Spherical aberration is a notorious form of point spread function aberration, and is one of the most difficult to combat. The artifact involves an axial asymmetry in the shape of the point spread function, which both increases the flare of the point spread function and decreases its brightness. A common problem in all forms of optical microscopy, spherical aberration is one of the primary causes of degraded resolution and signal loss in both confocal and widefield investigations. Detection of spherical aberration can be accomplished by focusing up and down through the specimen, observing asymmetry in the out-of-focus rings above and below a brightly fluorescent point-like detail (as illustrated in Figure 2). Alternatively, the artifact can be detected in an acquired image stack (in the x-z or y-z projections) by searching for axial asymmetry in the flare of blurred light around a fluorescent structure. A third technique useful for detection of spherical aberration is to acquire a point spread function image from a fluorescent bead mounted under similar optical conditions as the specimen, and to search for axial asymmetry in the flare of the point spread function.
If the specimen under observation is comparatively thick (greater than 10 micrometers), spherical aberration may be induced gradually as imaging occurs deeper within the specimen. Therefore, a bead mounted directly under the coverslip surface may not reveal spherical aberration in this instance. A suggested remedy is to acquire the point spread function image from a bead located near a desired image plane within the specimen by first exposing the specimen to a solution of fluorescent beads. However, this point spread function should not be utilized for deconvolution because scatter from the tissue will make the point spread function much noisier in most instances.
Spherical aberration is a result of an imperfection in the optical pathway of the imaging system. It can be due to defects in the objective, but more frequently the aberration occurs due to mismatches of refractive index in the optical media directly adjacent to the objective front lens element. Modern objectives are generally designed to correct and/or minimize spherical aberration only if they are used with the proper type and thickness of coverslip glass, and the proper immersion and mounting media. The optical properties of these materials are essential for the proper focusing of light by the objective (and the rest of the microscope optical train).
The images presented in Figure 2 (bovine pulmonary endothelial cells) were acquired with a widefield fluorescence imaging system under similar conditions except for a variation of the refractive index of the immersion oil. The raw image (maximum intensity projection) illustrated in Figure 2(a) was acquired with an immersion oil of 1.514 refractive index, and is free of appreciable spherical aberration. Figure 2(b) is the same image after deconvolution. A similar cell, acquired with an oil of higher refractive index (1.524), and exhibiting significant spherical aberration, is illustrated in Figure 2(c). The diffraction rings around points surrounding the cell are manifestations of the aberration. Following restoration of the raw image by iterative constrained deconvolution (Figure 2(d)), a horizontal line is introduced at the edge of a subvolume (to the right of arrowhead). This artifact is not present in the raw image (Figure 2(c)) and is, therefore, not caused by the imaging system.
Quite commonly in biological investigations, the refractive index of the immersion and mounting media are not identical, or even close. In these cases, two distortions may occur: spherical aberration and a scaling of z-axis distances. Both phenomena depend on focal depth, so features at different depths will demonstrate various amounts of spherical aberration and z-scaling artifacts. Although z-scaling does not affect resolution or signal intensity, it does represent a linear scaling of z-axis distance measurement by the ratio of the refractive indices of the mismatched media. To correct for this distortion, z-distances can be multiplied by a scalar compensation factor, and some software packages offer this feature. On the other hand, spherical aberration is difficult to correct and is therefore very tempting to ignore, but a small amount of attention to this issue can yield a large improvement in image quality, especially under low-light conditions such as in living cells.
Recently, several investigations have been targeted at digitally correcting for spherical aberration by deconvolving with a spherically aberrated point spread function. This requires deconvolution software that does not automatically preprocess the point spread function to render it axially symmetric. If this is the case, then the microscopist can precisely match the aberration in the image and point spread function by having on hand a "family" of empirical point spread functions with various degrees of spherical aberration and selecting the most appropriate point spread function for a given imaging condition. This type of computational correction may restore lost resolution to some extent, but it does not restore lost signal. Thus, the best mechanism to correct for spherical aberration is to eliminate the artifact beforehand by optical methods.
There are a variety of optical techniques and tricks employed by microscopists to correct for spherical aberration. One of the most common applications for specimens immersed in aqueous solutions is the dipping objective, which can directly enter the mounting medium without a coverslip. Because the immersion and mounting medium are identical, no refractive index mismatch is possible. However, distortion can still occur because of a refractive index mismatch between the specimen and the immersion medium or due to refractive index gradients within the specimen itself. An alternative method involves adjusting the refractive index of the immersion medium to compensate for the refractive index of the mounting medium. If the specimen is mounted in a medium of lower refractive index than glass (for example, glycerol or water-based media), then increasing the refractive index of the immersion medium will reduce or eliminate small degrees of spherical aberration. This technique enables a relatively aberration-free imaging condition up to a limited focal depth of about 10 to 15 micrometers from the coverslip when using an objective having a numerical aperture of 1.4 and the specimen is mounted in glycerol. Several commercial suppliers now offer immersion media with specified refractive indices that can be mixed to any desired intermediate value.
Another commonly employed technique is to use a specially corrected objective lens, such as the high numerical aperture water-immersion objectives now available for application with cover-slipped specimens. These objectives have a correction collar that enables compensation for refractive index variations between the lens elements and the specimen. Although they are very expensive (currently about $10,000), water-immersion objectives may provide the only method to eliminate spherical aberration when imaging deeper than 15 micrometers into a thick specimen. The correction collar on such objectives should not be confused with the variable-aperture correction collars found on less expensive darkfield objectives.
The Digital Image Sampling Interval
The proper sampling interval in the x, y, and z directions is important for good deconvolution results. It is standard practice to acquire samples at twice the resolvable spatial frequency, which conforms to the Nyquist sampling theorem (two samples per resolvable element are required for accurate detection of a signal). However, the Nyquist sampling frequency is really just the minimum necessary for a reasonable approximation of the real signal acquired by a discrete sampling mechanism. A higher sampling frequency produces superior restoration, especially when applying three-dimensional algorithms. In contrast, two-dimensional deblurring algorithms work most effectively when the sampling rate is lower in the z direction (when the spacing between optical sections is equal to or greater than the resolvable element).
In fluorescence microscopy, the resolvable element is often defined using the Rayleigh criterion. For example, with the dye FITC (emission peak at 520 nanometers), a 1.4 numerical aperture oil immersion objective, and a mounting/immersion medium with a refractive index of 1.51 (matching most optical glasses), the resolvable element size is 227 nanometers in the x-y plane and 801 nanometers in the z direction (according to the Rayleigh criterion). To sample at the Nyquist frequency under these conditions, the sampling interval should be half this value, or approximately 0.114 micrometers in the x-y plane and 0.4 micrometers in the z direction. To provide optimum results in image restoration, sampling at a smaller interval is recommended, perhaps 0.07 micrometers in the x-y plane and 0.2 micrometers in the z direction, under the same conditions.
It should be noted that these guidelines represent optimal settings and should be balanced by considering the specific preparation under investigation. As an example, the fluorescence signal may be so low (often seen in live cell experiments) that binning of CCD pixels is required, or events may occur so quickly that there is not sufficient time to finely sample in the z direction. In such cases, a suboptimal sampling interval will be required. Fortunately, restoration algorithms still work quite will under these conditions, although some changes in regularization may be necessary in some algorithms.
Ringing and Edge Artifacts
Ringing is an artifact chiefly encountered in the application of deblurring or inversion techniques, but it can also occur with iterative methods. The artifact has the appearance of dark and light ripples around bright features of an image, as illustrated in Figure 3, and can occur both in the z direction and in the x-y plane. When visualized in the z direction, ringing appears as a shadow in a deeper z-section, outlining a fluorescent structure.
The source of ringing is usually conversion of a discontinuous signal into or out of Fourier space. A number of related issues can produce signal discontinuities and therefore contribute to ringing. Discontinuities can occur at the edges of the image or of subvolumes of the image (Figure 2) or even at the edges of bright features (Figure 3). Another source of discontinuities is inadequate spatial sampling of the raw image or point spread function, a noisy image or point spread function, and a point spread function shape that is inappropriate to the image.
Each image presented in Figure 3 is a single representative optical section from a three-dimensional stack of images, and illustrates pyramid cell dendrites from fixed sections. The raw image is displayed in Figure 3(a), while Figure 3(b) is the same image field following iterative deconvolution. In the deconvolved image, significant ringing occurs (dark outline around fluorescent dendrite), most likely because of spherical aberration in the raw image, which is not matched in the point spread function. In the same image, noise amplification appears as a mottling of the background.
The best approach to avoid ringing is to ensure proper windowing of the Fourier transform. Although some commercial software packages have not addressed this issue, it is becoming more commonly implemented in the higher-end algorithms. Ringing can also be avoided by using a finer sampling interval in the image or point spread function, by smoothing the image or point spread function, by careful matching of aberrations in the point spread function with those of the image, or by adjustment of the point spread function parameters.

Ringing at the edges of an image can be suppressed by simply removing the edges. Many algorithms remove a guard band of 8 to 10 pixels or planes around an entire image. This operation requires blank space to be left above and below the fluorescent structures in the image. Blank space is advisable because blurred light from above and below an object can be reassigned and contributes to the signal for that object. However, the blank space can be artificially created, without loss of fidelity, by adding interpolated planes to the top and bottom of the image stack. The resulting cost in computer memory and processing time can be minimized by performing the interpolation in Fourier space.
Ringing at the edge of subvolumes is a similar issue (see Figure 2). Usually, the amount of subvolume overlap can be increased to remove the artifact. Alternatively, if enough random access memory (RAM) is installed, then the entire image can be processed as a single volume to avoid artifacts.
Noise Amplification and Excessive Smoothing
As previously discussed, noise amplification is an artifact caused by deblurring and inversion algorithms. The artifact also occurs with iterative algorithms as repeated convolution operations introduce high-frequency noise. Noise in deconvolved images is manifested as a distinctive mottling of the image that often is constant in every plane and is particularly noticeable in background areas. It can usually be suppressed by application of a smoothing filter or a regularization (roughness) filter. In cases where excessive noise is observed in a deconvolved image, then the first step toward a remedy is to ensure the point spread function is as noise-free as possible. Next, examine the algorithm filters and attempt to optimize their adjustable parameters so that image features larger than the resolution limit are maintained, while smaller variations are suppressed. Do not increase smoothing too much because excessive smoothing will degrade image resolution and contrast.
Disappearing and Exploding Features
Perhaps the most annoying artifacts of deconvolution are the apparent loss of very dim features or the blowing up (blooming or contrast explosion) of very bright features. These artifacts differ from those caused by excessive smoothing in that they affect specific features (Figure 4), as opposed to the image as a whole. In such a case, make an attempt to compare the effects of different algorithms on the appearance of the artifact (such as an inverse filter versus iterative algorithms, or classical versus statistical algorithms). If the artifact only appears with a single algorithm, then the cause may be algorithm instability or a specific effect of the algorithm on a particular specimen type. In cases where the effect occurs with several algorithms, then there are a variety of possible sources. When small, dim features of the image are disappearing, the cause is often a combination of nonnegativity and smoothing filters. This is likely to occur if there is excessive noise in the image or the point spread function, or if conditions are favorable to ringing. Noise and ringing can induce negative pixel values so that the nonnegativity constraint is invoked and features are dispersed. If this occurs, the smoothing filter may remove or smooth many of the remaining fragments, resulting in disappearance of the feature. The severity of the artifact can be compensated (or it can be eliminated entirely) by reducing noise in the image and the point spread function (with longer exposure times or by averaging), by eliminating point spread function mismatches, and by properly adjusting the smoothing filter.
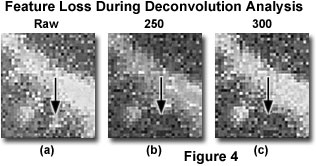
Figure 4 illustrates enlarged detail of an optical section similar to one displayed previously (Figure 3). The three enlargements are taken from the raw image, before deconvolution (Figure 4(a); Raw), and after deconvolution by an increasing number of iterations (250 and 300 iterations; Figure 4(b) and 4(c)). A small feature, indicated by the arrow, disappears as a result of the iterative deconvolution. This type of artifact can be avoided by correct application of the point spread function.
When bright features are expanding in a deconvolved image, then the source is probably pixel saturation. Raw images that contain a significant number of bright features will have this brightness extended even further during restoration. However, in very bright features, deconvolution algorithms can cause pixel values to exceed the highest value representable at a given bit depth. In effect, these pixels will saturate and will be assigned the maximum value. The feature will then become very bright, will appear to flatten, and may expand in size. The artifact can be avoided by utilizing a camera and software package that will allow greater bit depth and an algorithm that internally stores data as floating point numbers. Using these techniques expands computer memory requirements, but prevents the occurrence of such artifacts.
Specimen-Dependent Artifacts
The scientific literature is ripe with reports of deconvolution artifacts observed with some specimen types but not with others. In particular, some investigators have reported that filamentous structures are dispersed with one class of deconvolution algorithms but not with another. If a structural change is observed, then it is always advisable to compare the deconvolved and raw images. If close inspection reveals that a structural feature evident after deconvolution does not occur in the raw image, then the point spread function parameters should be examined to determine their correct settings, and the point spread function should also be scrutinized for noise. If the problem persists, then the entire algorithm is suspect and the effects of different algorithms on the appearance of the artifact should be compared. This procedure will verify whether a particular specimen is restored to a satisfactory degree by a given algorithm.
When an apparent artifact is visible in both deconvolved and raw images, then some aspect of specimen preparation or optical aberration is implicated. In particular, immunofluorescence staining is often discontinuous along cytoskeletal filaments (actin filaments, microtubules, and intermediate filaments). Several sources can contribute to this problem. One is that cytoskeleton-associated proteins may mask cytoskeletal filaments, so that antibody accessibility is variable along the filament. Another source is the fixatives utilized in immunocytochemistry, which often do not faithfully preserve filamentous structures. For example, microtubules may fragment during formaldehyde or methanol fixation. A more faithful fixative such as glutaraldehyde can be employed, but at the expense of antigenicity. Optimal fixation methods are described in a variety of literature sources and textbooks.
A common source of specimen-dependent artifacts derives from refractive index gradients in the specimen itself. These cause lensing effects in the specimen before light reaches the objective and, therefore, may distort the image. Some specimens (for instance, embryos and thick tissues) have yolk granules or other organelles whose refractive index is significantly different from the surrounding cytoplasm. In addition, there may be refractive index gradients in the mounted specimen caused by heterogeneous mixing of the mounting medium. This artifact is particularly likely if the specimen is mounted in a medium in which it was not previously immersed. Computational methods for correcting such heterogeneities may be available in the future, but it is always a good practice to minimize these artifacts by thoroughly immersing the specimen in a mounting medium that is well matched to the specimen's own refractive index. As an additional measure, it is wise to adjust the refractive index of the immersion medium (when possible) to compensate for that of the mounting medium.
Horizontal and Vertical Lines
Probably the most common artifacts of deconvolution microscopy are horizontal and vertical lines in the x, y, and z-axes. In many instances, these lines can be observed in the raw image when it is carefully examined, indicating that they are not a result of the deconvolution operations, but are enhanced by the algorithms. Lines or bands can also result from edge artifacts at the borders between subvolumes, a form of ringing. In any case, such artifacts are difficult to mistake for biological structures and can be easily removed.
Horizontal or vertical lines in the x-y plane are often due to column defects in the CCD sensor utilized to record the image. If one pixel in the read register of the chip has a defect or if transfer to that pixel is less efficient, then the result may appear as a line perpendicular to the read register. This line is then enhanced by the deconvolution operation. Problems such as this can often be corrected with a flat-fielding operation, also termed shading or background correction, and is included in most deconvolution software packages.
Vertical lines observed in the x-z or y-z views (termed the z-lines) are due to variation in the response characteristics of individual pixels. Each pixel has a slightly different gain and offset from its neighbors. In extreme cases, there are bad pixels whose photon response deviates significantly from their neighbors. Often, the same pixel systematically deviates from its neighbors throughout a stack of images, leaving a z-line. The problem can be corrected by flat-field operations or by specialized bad pixel routines that search out these culprits and replace them with the mean value of their immediate neighbors.
In contrast, horizontal lines in x-z or y-z views represent entire planes in the image stack that are uniformly brighter than their neighbors. This problem is due to fluctuations in the illumination system. In situations where the arc lamp power output deviates during data collection, then this variation will be recorded as a systematic difference in fluorescence intensity between planes. In addition, the arc in a lamp can wander over the surface of the electrodes, inducing time-dependent spatial heterogeneities in the illumination of the specimen. These events will be accentuated by deconvolution, but can be observed in the raw image. Both problems can usually be minimized by replacing the arc lamp.
If lamp fluctuations continue to be a problem even with a new arc lamp, then a direct measure of arc lamp power fluctuation combined with a polynomial fit of summed pixel intensities plane-by-plane can be employed to apply a correction to the raw image. Some form of this type of correction is included in a majority of the commercially available deconvolution packages. The second problem, changes in the illumination pattern due to arc wandering, is difficult to correct by image processing, but can be eliminated by installing a fiber-optic scrambler between the arc lamp and the microscope vertical illuminator.