Diffraction of Light
Diffraction is a term that defines the phenomena of waves interacting with particles. In this piece, we discuss diffraction of light waves, from diffraction examples to light diffraction equations.
What Is Diffraction?
We classically think of light as always traveling in straight lines, but when light waves pass near a barrier they tend to bend around that barrier and become spread out. The definition of diffraction is the spreading of waves as they pass through or around an obstacle. More specifically when applied to light, diffraction of light occurs when a light wave passes by a corner or through an opening or slit that is physically the approximate size of, or even smaller than that light’s wavelength.

Diffraction Examples
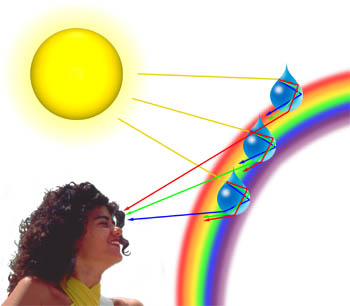
A very simple demonstration of diffraction of waves can be conducted by holding your hand in front of a light source and slowly closing two fingers while observing the light transmitted between them. As the fingers approach each other and come very close together, you begin to see a series of dark lines parallel to the fingers. The parallel lines are actually diffraction patterns. This phenomenon can also occur when light is “bent” around particles that are on the same order of magnitude as the wavelength of the light. A good example of this is the diffraction of sunlight by clouds that we often refer to as a silver lining, illustrated in Figure 1 with a beautiful sunset over the ocean.
We can often observe pastel shades of blue, pink, purple, and green in clouds that are generated when light is diffracted from water droplets in the clouds. The amount of diffraction depends on the wavelength of light, with longer wavelengths being diffracted at a greater angle than shorter ones (in effect, red light are diffracted at a higher angle than is blue and violet light). As a light wave traveling through the atmosphere encounters a droplet of water, as illustrated below, it is first refracted at the water-to-air interface, then it is reflected as it again encounters the interface. The beam, still traveling inside the water droplet, is once again refracted as it strikes the interface for a third time. This last interaction with the interface refracts the light back into the atmosphere, but it also diffracts a portion of the light as illustrated below. This diffraction element leads to a phenomenon known as Cellini’s halo (also known as the Heiligenschein effect) where a bright ring of light surrounds the shadow of the observer’s head.
What Is the Difference Between Diffraction and Scattering?
The terms diffraction and scattering are often used interchangeably and are considered to be almost synonymous. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a diffraction grating) produces an orderly diffraction of light in a diffraction pattern. In the real world, most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light.
The Single-Slit Optical Diffraction Experiment
One of the classic and most fundamental concepts involving diffraction of light waves is the single-slit optical diffraction experiment, first conducted in the early nineteenth century. When a light wave propagates through a slit (or aperture) the result depends upon the physical size of the aperture with respect to the wavelength of the incident beam. This is illustrated in Figure 3 assuming a coherent, monochromatic wave emitted from point source S, similar to light that would be produced by a laser, passes through aperture d and is diffracted, with the primary incident light beam landing at point P and the first secondary maxima occurring at point Q.
![An illustration showing diffraction of coherent laser light]](https://static1.olympus-lifescience.com/data/Image/olympusmicro/primer/images/diffraction/fresnel.jpeg?rev=9C86)
As shown in the left side of the figure, when the wavelength (λ) is much smaller than the aperture width (d), the wave simply travels onward in a straight line, just as it would if it were a particle or no aperture were present. However, when the wavelength exceeds the size of the aperture, we experience diffraction of the light according to the equation:
sinθ = λ/d
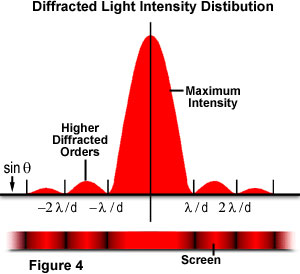
Where θ is the angle between the incident central propagation direction and the first minimum of the diffraction pattern. The experiment produces a bright central maximum that is flanked on both sides by secondary maxima, with the intensity of each succeeding secondary maximum decreasing as the distance from the center increases. Figure 4 illustrates this point with a plot of beam intensity versus diffraction radius. Note that the minima occurring between secondary maxima are located in multiples of π.
This experiment was first explained by Augustin Fresnel who, along with Thomas Young, produced important evidence confirming that light travels in waves. From the figures above, we see how a coherent, monochromatic light (in this example, laser illumination) emitted from point L is diffracted by aperture d. Fresnel assumed that the amplitude of the first order maxima at point Q (defined as εQ) would be given by the equation:
dεQ = α(A/r)f(χ)d
where A is the amplitude of the incident wave, r is the distance between d and Q, and f(χ) is a function of χ, an inclination factor introduced by Fresnel.
Diffraction of Light
Explore how a beam of light is diffracted when it passes through a narrow slit or aperture. Adjust the wavelength and aperture size and observe how this affects the diffraction intensity pattern.
Diffraction of light plays a paramount role in limiting the resolving power of any optical instrument (for example: cameras, binoculars, telescopes, microscopes, and the eye). The resolving power is the optical instrument’s ability to produce separate images of two adjacent points. This is often determined by the quality of the lenses and mirrors in the instrument as well as the properties of the surrounding medium (usually air). The wave-like nature of light forces an ultimate limit to the resolving power of all optical instruments.
Circular Aperture Diffraction Equations
Our discussions of diffraction have used a slit as the aperture through which light is diffracted. However, all optical instruments have circular apertures, for example the pupil of an eye or the circular diaphragm and lenses of a microscope. Circular apertures produce diffraction patterns similar to those described above, except the pattern naturally exhibits a circular symmetry. Mathematical analysis of the diffraction patterns produced by a circular aperture is described by the diffraction equation:
sinθ(1) = 1.22(λ/d)
where θ(1) is the angular position of the first order diffraction minima (the first dark ring), λ is the wavelength of the incident light, d is the diameter of the aperture, and 1.22 is a constant. Under most circumstances, the angle θ(1) is very small so the approximation that the sin and tan of the angle are almost equal yields:
θ(1) ≅ 1.22(λ/d)
From these equations, it becomes apparent that the central maximum is directly proportional to λ/d, making this maximum more spread out for longer wavelengths and for smaller apertures. The secondary minima of diffraction set a limit to the useful magnification of objective lenses in optical microscopy due to inherent diffraction of light by these lenses. No matter how perfect the lens may be, the image of a point source of light produced by the lens is accompanied by secondary and higher order maxima. This could be eliminated only if the lens had an infinite diameter. Two objects separated by a distance less than θ(1) cannot be resolved, no matter how high the power of magnification. While these equations were derived for the image of a point source of light an infinite distance from the aperture, it is a reasonable approximation of the resolving power of a microscope when d is substituted for the diameter of the objective lens.
Thus, if two objects reside a distance D apart from each other and are at a distance L from an observer, the angle (expressed in radians) between them is:
θ = D / L
which leads us to be able to condense the last two equations to yield:
D(0) = 1.22(λL/d)
Where D(0) is the minimum separation distance between the objects that will allow them to be resolved. Using this diffraction equation, the human eye can resolve objects separated by a distance of 0.056 millimeters, however the photoreceptors in the retina are not quite close enough together to permit this degree of resolution, and 0.1 millimeters is a more realistic number under normal circumstances.
The resolving power of optical microscopes is determined by a number of factors including those discussed, but in the most ideal circumstances, this number is about 0.2 micrometers. This number must take into account optical alignment of the microscope, quality of the lenses, as well as the predominant wavelengths of light used to image the specimen. While it is often not necessary to calculate the exact resolving power of each objective (and would be a waste of time in most instances), it is important to understand the capabilities of the microscope lenses as they apply to the real world.
Sorry, this page is not
available in your country.