The quartz wedge is a simple, semi-quantitative compensator designed around a crystalline block of quartz cut with an elongated wedge angle so that the optical axis of the quartz is oriented either parallel or perpendicular to the edge of the birefringent crystal. The optical path difference between the orthogonally polarized fast and slow wavefronts traversing the wedge is a continuously variable function of the thickness along the wedge hypotenuse. A typical quartz wedge has an effective range of 4 orders (approximately 500 to 2000 nanometers) and is commonly employed for qualitative retardation measurements of petrographic specimens (rock and mineral thin sections) or other birefringent materials whose retardation value falls within the wedge limits. The quartz wedge compensator is also employed for the routine determination of the direction of anisotropy (crystalline fast and slow axes orientation) in birefringent specimens.
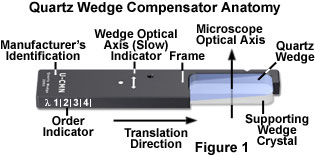
The anatomy of a typical quartz wedge compensator is illustrated in Figure 1. In order to fabricate the compensator, a rectangular slab of quartz approximately 15 × 35 millimeters in size is ground into a wedge with a thickness ranging between 0.1 and 0.25 millimeters from the thin to the thick dimensions, respectively. Most wedges are cut so that the vibration direction of the fast (ordinary) wavefront is parallel to the long crystalline dimension and the slow (extraordinary) vibration direction is parallel to the short dimension. The finished wedge is cemented to a thicker section of wedge or plane parallel support and placed in a black rectangular frame having the standard DIN dimensions (6 × 20 millimeters). The direction of the slow optical axis is indicated on the supporting frame (usually marked slow or γ; see Figure 1), as are the manufacturer's specifications. In addition, the approximate order of the wedge at various positions in the optical train is indicated by a graduated scale on the side of the frame.
When a quartz wedge compensator frame is placed at a 45-degree angle between the transmission azimuths of crossed polarizers on a light table (or at low magnification within a microscope) and illuminated with monochromatic light, a series of bright and dark parallel fringes will be observed perpendicular to the long axis of the crystal. The dark fringes correspond to optical path differences of zero, one wavelength, two wavelengths, etc., while the bright fringes represent path differences of one-half wavelength, three-halves wavelength, and so on. For example, using monochromatic blue light (450 nanometers; Figure 2(b)), the dark fringes occur at optical path differences of zero, 450, 900, 1350, and 1800 nanometers. Similarly, bright fringes (in blue light) have optical path differences of 225, 675, 1124, and 1575 nanometers. For monochromatic light of longer wavelengths (green and red; Figures 2(c) and 2(d)), the distance between the bright and dark fringes increases.
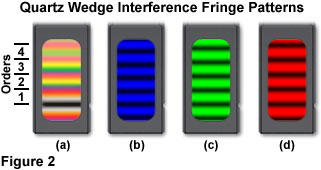
Trans-illuminating the quartz wedge (either in a microscope or between crossed polarizers) in a similar manner with the full spectrum of white light produces a series of transverse bands having interference colors that progress up the Michel-Levy chart with increasing wedge thickness (Figure 2(a)). On the thin end of the wedge, the first prominent band is black (termed first-order black) where retardation is negligible. Interference colors are grouped into classifications, termed orders, with a wavelength of 551 nanometers (the region of the solar spectrum that appears the brightest) being the size of each individual order. Colors in the first order correspond to optical path differences ranging from zero to 551 nanometers, while colors in the second order are those having path differences from 551 to 1102 nanometers (third and fourth orders successively add 551 nanometers to the second order size). As the order number increases, the interference colors seen through a quartz wedge compensator lose saturation and gradually approximate a white hue, termed higher-order white.
In practice, the quartz wedge compensator is inserted at a 45-degree angle (with respect to the polarizer and analyzer) into the microscope optical train through a DIN slot located in the microscope nosepiece or an intermediate tube positioned between the frame and the observation tubes. As the wedge compensator is slowly translated farther into the light path, the optical path difference of wavefronts passing through increases to generate a succession of interference colors, as previously described. The number of interference color orders produced by a quartz wedge is a function of the wedge inclination angle. Greater angles produce a larger number of orders per unit length. By rotating the polarized microscope circular stage, a specimen is oriented in a subtractive alignment with respect to the compensator, and the quartz wedge inserted until the birefringent area of the specimen appears compensated (extinct). The specimen optical path difference can be estimated by comparing the black (zeroth order) fringe appearing in the compensated specimen area to the colored fringe in the immediately adjacent region. This interference color can be located on a Michel-Levy chart to ascertain the optical path difference with an accuracy of 100-200 nanometers. Although many quartz wedges are engraved with an optical path difference scale on the frame (see Figure 1), the compensator has a wide error range and is generally employed as a qualitative tool to determine only the approximate optical path difference.
Green interference filters (550 or 556 nanometer) should be removed from the optical path before attempting relative retardation measurements with a quartz wedge. In using low power objective (2x, 4, and 10x), ensure that the condenser aperture iris diaphragm is closed to its smallest opening size or the specimen will not be compensated (turn dark or black), even when the birefringent feature and quartz wedge are properly overlapped to achieve extinction. If the feature of interest does not become dark throughout the entire range of the quartz wedge, check to ascertain that the birefringent feature is rotated 45-degrees from the extinction position in crossed polarizers before inserting the wedge. In many cases, the specimen can also be rotated by 90 degrees with the wedge in place to achieve extinction. However, if the specimen feature is not extinguished by the quartz wedge after a 90-degree rotation, then the retardation value is outside the wedge measuring range and another technique must be implemented in order to quantitatively assess the optical path difference.

The examination of optical path difference in three unrelated specimens is presented in Figure 3 using the quartz wedge technique. In all cases, the specimens were oriented with their slow axes either parallel or perpendicular to the quartz wedge optical axis. A thin section of micropegmatite granite revealing the grain structure in polarized light is illustrated in Figure 3(a). The birefringent grain in the central portion of the image can be compensated (Figure 3(b)) by inserting a quartz wedge into the optical path until the region corresponding to first order gray (approximately 250 nanometers) is reached. This indicates that the relative retardation or optical path difference of the grain is close to 250 nanometers.
Birefringent fibers are excellent candidates for relative retardation analysis with a quartz wedge. A pair of nylon fibers exhibits first and second order interference colors when observed between crossed polarizers (Figure 3(c) at a 45-degree angle, and can be compensated by inserting a quartz wedge into the optical path to a point just between first order magenta and second order blue (Figure 3(d)). The relative retardation of the nylon fibers is approximately 600 nanometers. Finally, a thick crystal (2 millimeters) of lanthanum aluminate reveals a significant amount of twinning and interference colors in the higher orders in polarized light (Figure 3(e)), which is compensated (Figure 3(f)) by inserting a quartz wedge completely into the optical path at the highest (fourth) order. The optical path difference of the crystal is so large (approximately 2000 nanometers; due primarily to the excessive thickness) that it can only be measured at the upper limit of the quartz wedge's range.
In summary, the quartz wedge is an excellent tool for determining the optical sign of a birefringent specimen when high order interference colors are present. The thin edge of the wedge is first inserted into the microscope, and increasingly higher order interference colors are observed as thicker portions of the wedge cross the field of view. Specimens having an optical path difference ranging up two 2000 nanometers can be qualitatively inspected with the quartz wedge, but more accurate measurements of relative retardation can only be achieved with a more accurate device, such as a de Sénarmont or Berek compensator.